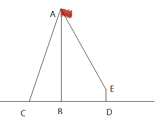
【題目】數學活動課上老師帶領全班學生測量旗桿高度.如圖垂直于地面的旗桿頂端A垂下一根繩子.小明同學將繩子拉直釘在地上，繩子末端恰好在點C處且測得旗桿頂端A的仰角為75°；小亮同學接著拿起繩子末端向前至D處，拉直繩子，此時測得繩子末端E距離地面1.5 m且與旗桿頂端A的仰角為60°根據兩位同學的測量數據，求旗桿AB的高度.（參考數據:sin75°≈0.97，cos75°≈0.26,sin60°≈0.87,結果精確到1米）
輕松課堂單元期中期末專題沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】某超市為了答謝顧客發起活動：凡在本超市一次性購物滿100元的顧客，當天均可憑購物小票參與一次抽獎活動，獎品是三種瓶裝飲品：紅酒、啤酒和酸奶，抽獎規則如下：
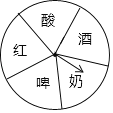
①如圖，是一個材質均勻可自出轉動的轉盤，轉盤被等分成五個扇形區域，各區域上分別寫有“紅”、“啤”、“酒”、“酸”、“奶”字樣；
②參與一次獎活動的顧客可以進行兩次“隨機轉動”，但若轉盤停止時指針指向兩邊區域的邊界則可以重新轉動轉盤，直到指針停到有字的區域才算完成了這次隨機轉動；
③顧客參與一次抽獎活動，記錄兩次指針所指區域對應的字，若這兩個字和某種獎品名稱對應的兩個字相同（與字的順序無關），便可獲得相應獎品一瓶；若兩字不能組成一種獎品名時，不能獲得任何獎品，根據以上規則，回答下列問題：
（1）求只做一次“隨機轉動”指針指向“酒“字的概率；
（2）請用列表或畫樹狀圖的方法求顧客參與一次抽獎活動獲得一瓶紅酒的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
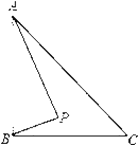
【題目】如圖，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC內部的一個動點，且滿足∠PAB=∠PBC，則線段CP長的最小值為（ ）
A. 2 B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
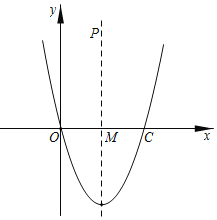
【題目】已知拋物線頂點坐標為（2，﹣4），且與x軸交于原點和點C，對稱軸與x軸交點為M．
（1）求拋物線的解析式；
（2）A點在拋物線上，且A點的橫坐標為﹣2，在拋物線對稱軸上找一點B，使得AB與CB的差最大，求B點的坐標；
（3）P點在拋物線的對稱軸上，且P點的縱坐標為8．探究：在拋物線上是否存在點Q使得O、M、P、Q四點共圓，若存在求出Q點坐標；若不存在請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
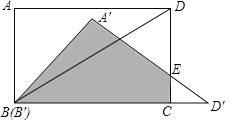
【題目】如圖，在矩形ABCD中，AB＝6cm，AD＝8cm，連接BD，將△ABD繞B點作順時針方向旋轉得到△A′B′D′（B′與B重合），且點D′剛好落在BC的延長上，A′D′與CD相交于點E．
（1）求矩形ABCD與△A′B′D′重疊部分（如圖中陰影部分A′B′CE）的面積；
（2）將△A′B′D′以2cm/s的速度沿直線BC向右平移，當B′移動到C點時停止移動．設矩形ABCD與△A′B′D′重疊部分的面積為ycm2，移動的時間為x秒，請你求出y關于x的函數關系式，并指出自變量x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
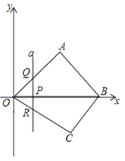
【題目】如圖,在平面直角坐標系中,四邊形
的頂點
是坐標原點，點
在第一象限,點
在第四象限,點
在
軸的正半軸上，
且
.
(1)求點和點的坐標;
(2)點
是線段
上的一個動點(點不與點
重合) ,以每秒
個單位的速度由點向點運動，過點的直線
與
軸平行,直線交邊
或邊
于點
,交邊
或邊
于點
,設點.運動時間為
,線段
的長度為
,已知
時,直線恰好過點 .
①當
時,求關于的函數關系式;
②點出發時點
也從點出發,以每秒個單位的速度向點運動，點停止時點也停止.設
的面積為
,求與的函數關系式;
③直接寫出②中的最大值是 .
查看答案和解析>>
科目：初中數學 來源： 題型：
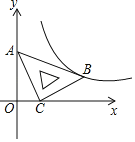
【題目】在平面直角坐標系xOy中，將一塊含有45°角的直角三角板如圖放置，直角頂點C的坐標為（1，0），頂點A的坐標為（0，2），頂點B恰好落在第一象限的雙曲線上，現將直角三角板沿x軸正方向平移，當頂點A恰好落在該雙曲線上時停止運動，則此時點C的對應點C′的坐標為（ ）
A.（
，0）B.（2，0）C.（
，0）D.（3，0）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程
。
（1）求證：方程有兩個不相等的實數根；
（2）若△ABC的兩邊AB、AC的長是方程的兩個實數根，第三邊BC的長為5。當△ABC是等腰三角形時，求k的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
