

 ▲ ,
▲ ,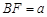 ,
,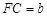 ,DE與BC間的距離為
,DE與BC間的距離為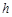 .請證明S2=4S1 S2.
.請證明S2=4S1 S2.
 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:初中數學 來源: 題型:
 的圓孔,需對鐵片進行處理(規定鐵片與圓孔有接觸時鐵片不能穿過圓孔);
的圓孔,需對鐵片進行處理(規定鐵片與圓孔有接觸時鐵片不能穿過圓孔);


 時,判斷直角梯形鐵片EBAF能否穿過圓孔,并說明理由;
時,判斷直角梯形鐵片EBAF能否穿過圓孔,并說明理由; 查看答案和解析>>
科目:初中數學 來源: 題型:
 中,
中, 、
、 、
、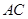 三邊的長分別為
三邊的長分別為 、
、 、
、 ,求這個三角形的面積.小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點
,求這個三角形的面積.小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點 (即
(即 三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求
三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求 的高,而借用網格就能計算出它的面積.
的高,而借用網格就能計算出它的面積. 的面積直接填寫在橫線上._________________________思維拓展:
的面積直接填寫在橫線上._________________________思維拓展: 面積的方法叫做構圖法.若
面積的方法叫做構圖法.若 三邊的長分別為
三邊的長分別為 、
、 、
、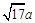 (
(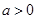 ),請利用圖②的正方形網格(每個小正方形的邊長為
),請利用圖②的正方形網格(每個小正方形的邊長為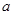 )畫出相應的
)畫出相應的 ,并求出它的面積.探索創新:
,并求出它的面積.探索創新: 三邊的長分別為
三邊的長分別為 、
、 、
、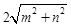 (
(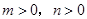 ,且
,且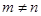 ),試運用構圖法求出這三角形的面積.
),試運用構圖法求出這三角形的面積.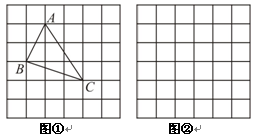
查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江省杭州市蕭山瓜瀝片八年級12月月考數學卷 題型:解答題
問題背景:在△ABC中,AB、BC、AC三邊的長分別為、、, 求這個三角形的面積.
求這個三角形的面積.
小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求△ABC的高,而借用網格就能計算出它的面 積.
積.
【小題1】(1)請你將△ABC的面積直接填寫在橫線上.____ ▲__ _____
_____
【小題2】(2)我們把上述求△ABC面積的方法叫做構圖法.若△ABC三邊的長分別為a、2a、a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
【小題3】(3)若△ABC三邊的長分別為、、2(m>0,n>0,且m≠n),試運用構圖法求出這三角形的面積.
查看答案和解析>>
科目:初中數學 來源:2012屆浙江省金華地區九年級下學期第一次月考數學卷 題型:解答題
問題背景
【小題1】(1)如圖1,△ABC中,DE∥BC分別交AB,AC于D,E兩點,過點E作EF∥AB交BC于點F.請按圖示數據填空: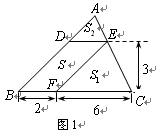
四邊形DBFE的面積 ▲ ,
▲ ,
△EFC的面積S1= ▲ ,
△ADE的面積S2= ▲ .
探究發現
【小題2】(2)在(1)中,若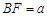 ,
, ,DE與BC間的距離為
,DE與BC間的距離為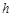 .請證明S2=4S1 S2.
.請證明S2=4S1 S2.
拓展遷移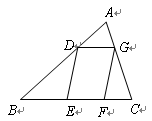
【小題3】(3)如圖2,平行四邊形DEFG的四個頂點在△ABC的三邊上,若△ADG、△DBE、△GFC的面積分別為2、5、3,試利用(2)中的結論求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com