
【題目】閱讀下面材料,完成![]() 題.
題.
數學課上,老師出示了這樣一道題:
如圖1,在![]() 中,
中,![]() 點
點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,
上,![]() .點
.點![]() 在
在![]() 延長線上,連接
延長線上,連接![]() .探究線段
.探究線段![]() 與
與![]() 的數量關系并證明.
的數量關系并證明.
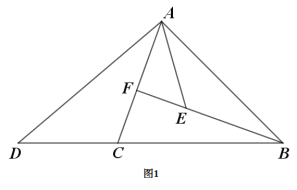
同學們經過思考后,交流了自己的想法:
小明:“通過觀察和度量,發現![]() 與
與![]() 相等.”
相等.”
小亮:“通過觀察和度量,發現![]() 與
與![]() 也相等.”
也相等.”
小偉:“通過邊角關系構造輔助線,經過進一步推理, 可以得到線段![]() 與
與![]() 的數量關系.”
的數量關系.”
老師:“保留原題條件,延長圖1中的![]() 與
與![]() 相交于點
相交于點![]() (如圖2),若知道
(如圖2),若知道![]() 與
與![]() 的數量關系,可以求出
的數量關系,可以求出![]() 的值.”
的值.”
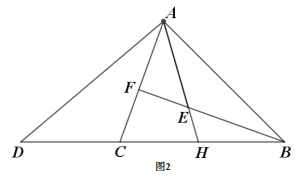
(1)求證:![]() ;
;
(2)求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)如圖2,若![]() 則
則![]() 的值為 (用含
的值為 (用含![]() 的式子表示).
的式子表示).
科目:初中數學 來源: 題型:
【題目】已知二次函數![]()
![]() ,一次函數
,一次函數![]() ,
,
有下列結論:
①當![]() 時,
時,![]() 隨
隨![]() 的增大而減小;
的增大而減小;
②二次函數![]()
![]() 的圖象與
的圖象與![]() 軸交點的坐標為
軸交點的坐標為![]() 和
和![]() ;
;
③當![]() 時,
時,![]() ;
;
④在實數范圍內,對于![]() 的同一個值,這兩個函數所對應的函數值
的同一個值,這兩個函數所對應的函數值![]() 均成立,則
均成立,則![]() .
.
其中,正確結論的個數是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
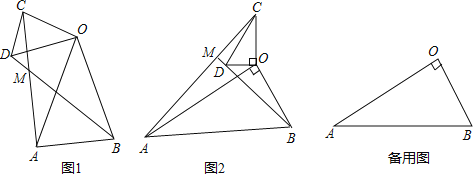
【題目】(1)問題發現
如圖1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,連接AC,BD交于點M.填空:
①![]() 的值為 ;
的值為 ;
②∠AMB的度數為 .
(2)類比探究
如圖2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,連接AC交BD的延長線于點M.請判斷![]() 的值及∠AMB的度數,并說明理由;
的值及∠AMB的度數,并說明理由;
(3)拓展延伸
在(2)的條件下,將△OCD繞點O在平面內旋轉,AC,BD所在直線交于點M,若OD=1,OB=![]() ,請直接寫出當點C與點M重合時AC的長.
,請直接寫出當點C與點M重合時AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強公民的節約意識,合理利用天然氣費源,某市自1月1日起對市區民用管道天然氣價格進行調整,實行階梯式氣價,調能后的收費價格如表所示:
每月用氣量 | 單價(元/m3) |
不超出75m3的部分 | 2 |
超出75 m3不超過125 m3的部分 | a |
超出125 m2的部分 | a+0.5 |
(1)若某戶3月份用氣量為60 m3,則應交費多少元?
(2)調價后每月支付燃氣費用y(元)與每月用氣量x(m3)的函數關系如圖所示,求a的值及線段AB對應的一次函數的表達式;
(3)求射線BC對應的一次函數的表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,在正方形
,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,
,
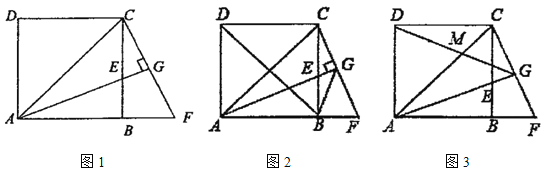
(1)求證:![]() ;
;
(2)如圖![]() ,連接
,連接![]() 、
、![]() ,求證
,求證![]() 平分
平分![]() ;
;
(3)如圖![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() , 求
, 求![]() 的值。
的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
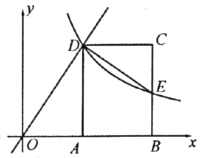
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() ,
,![]() 在
在![]() 軸的正半軸上,頂點
軸的正半軸上,頂點![]() 在直線
在直線![]() 位于第一象限的圖像上,反比例函數
位于第一象限的圖像上,反比例函數![]() 的圖像經過點
的圖像經過點![]() ,交
,交![]() 于點
于點![]() ,
,![]() .
.
(1)如果![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)連接![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
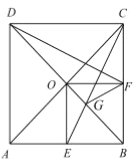
【題目】如圖,在邊長為1的正方形![]() 中,對角線
中,對角線![]() ,
,![]() 相交于點
相交于點![]() ,點
,點![]() ,點
,點![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,得到以下四個結論:①
,得到以下四個結論:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正確的結論是________(填寫序號).
,其中正確的結論是________(填寫序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠BAC=90°,AB=AC,點D,E分別在邊AB,AC上,AD=AE,連接DC,BE,點P為DC的中點,
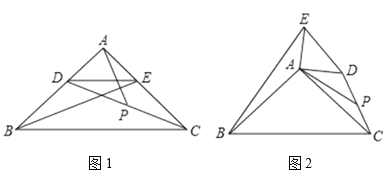
(1)(觀察猜想)圖1中,線段AP與BE的數量關系是 ,位置關系是 .
(2)(探究證明)把△ADE繞點A逆時針旋轉到圖2的位置,(1)中的猜想是否仍然成立?若成立請證明,否請說明理由;
(3)(拓展延伸)把△ADE繞點A在平面內自由旋轉,若AD=4,AB=10,請直接寫出線段AP長度的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com