【題目】某公司欲招聘一名部門經理，對甲、乙、丙三名候選人進行了三項素質測試．各項測試成績如表格所示：
測試項目 | 測試成績 | ||
甲 | 乙 | 丙 | |
專業知識 | 74 | 87 | 90 |
語言能力 | 58 | 74 | 70 |
綜合素質 | 87 | 43 | 50 |
（1）根據實際需要，公司將專業知識、語言能力和綜合素質三項測試得分按4：3：1的比例確定每個人的測試總成績，此時誰將被錄用？
（2）請重新設計專業知識、語言能力和綜合素質三項測試得分的比例來確定每個人的測試總成績，使得乙被錄用，若重新設計的比例為x：y：1，且x+y+1＝10，則x＝ ，y＝ ．（寫出x與y的一組整數值即可）
【答案】（1）此時丙將被錄用；（2）1，8．（答案不唯一）
【解析】
（1）先根據加權平均數的計算公式求出三人的總成績，再比較大小即可得；
（2）先分析乙的三項成績，使其成績高的項目所占權重盡可能大，再根據
得出一組x與y的整數值，然后利用加權平均數的計算公式進行檢驗即可．
（1）甲的總成績：
，乙的總成績：
，丙的總成績：
由此可知，丙的總成績最高
故此時丙將被錄用；
（2）∵乙的專業能力為87分，位于第二，語言能力74分，位于第一，而綜合素質43分，位于第三
∴要使得乙被錄用，則語言能力所占的權重要盡可能大，即y盡可能大
∴
因此，
即可
經過計算得：當時，甲的總成績：
，乙的總成績：
，丙的總成績：
，符合要求
故答案為：1，8．（答案不唯一）
科目：初中數學 來源： 題型：
【題目】如圖，在每個小正方形的邊長都是
的正方形網格中，
的三個頂點都在小正方形的格點上．將繞點
旋轉
得到
（點
、
分別與點
、
對應），連接
，
．
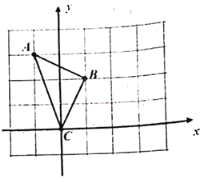
（1）請直接在網格中補全圖形；
（2）四邊形
的周長是________________（長度單位）
（3）直接寫出四邊形是何種特殊的四邊形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】國慶假期期間，某單位8名領導和320名員工集體外出進行素質拓展活動，準備租用45座大車或30座小車．若租用2輛大車3輛小車共需租車費1700元；若租用3輛大車2輛小車共需租車費1800元
（1）求大、小車每輛的租車費各是多少元？
（2）若每輛車上至少要有一名領導，每個人均有座位，且總租車費用不超過3100元，求最省錢的租車方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在等腰
中，
，直線
過點
且
．
是
上一點，過作
垂足為
，過作
垂足為
，已知
．
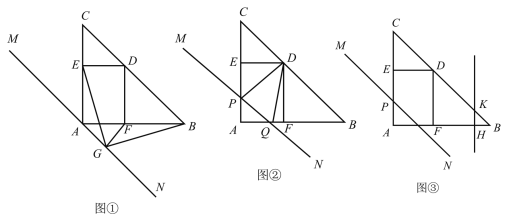
（1）如圖①，在直線上有一點
，連接
，且
，求證：
；
（2）如圖②，將沿
方向平移，分別交
于
，
兩點，當
時，求
的面積；
（3）如圖③，設直線從點出發沿方向平移的速度為每秒1個單位，與
交于點，同時有一動點
從
點出發以相同的速度向點運動，過作
交
于
，設運動時間為
，當到達點時所有運動停止，問是否存在以、、為頂點的三角形是等腰三角形？若存在，直接寫出的值；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，菱形ABCD中，點P是CD的中點，∠BCD=60°，射線AP交BC的延長線于點E，射線BP交DE于點K，點O是線段BK的中點．
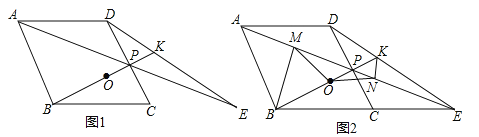
（1）求證：△ADP≌△ECP；
（2）若BP=nPK，試求出n的值；
（3）作BM丄AE于點M，作KN丄AE于點N，連結MO、NO，如圖2所示，請證明△MON是等腰三角形，并直接寫出∠MON的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（題文）圖1是一個長為2a，寬為2b的長方形，沿圖中虛線剪開分成四塊小長方形，然后按圖2的形狀拼成一個正方形.
圖2的陰影部分的正方形的邊長是______.
用兩種不同的方法求圖中陰影部分的面積.
（方法1）
= ____________；
（方法2）= ____________；
(3) 觀察圖2，寫出(a+b)2,(a-b)2,ab這三個代數式之間的等量關系；
根據
題中的等量關系，解決問題：若m+n=10,m-n=6，求mn的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
