
【題目】甲乙兩車間共120人,其中甲車間人數比乙車間人數的4倍少5人.
(1)求甲、乙兩車間各有多少人?
(2)若從甲、乙兩車間分別抽調工人,組成丙車間研制新產品,并使甲、乙、丙三個車間的人數比為13∶4∶7,那么甲、乙兩車間要分別抽調多少工人?
【答案】
(1)
解:設乙有x 人 則甲有4x-5
由題意可得 x+4x-5=120
x=25人
所以甲有4×25-5=95人 乙有25人.
(2)
由人數比例可知抽調以后,各車間人數為
甲車間人數= ![]() (人)
(人)
乙車間人數= ![]() (人)
(人)
丙車間人數= ![]() (人)
(人)
設甲車間抽調了x人,則乙車間抽調了35-x人,
由題意可得(65+x)=4(35-x+20)-5
解得,x=30,則35-x=35-30=5
答:甲車間抽調了30人,乙車間抽調了5人.
【解析】找出題目中的等量關系是難點(1)關系式為:甲車間人數+乙車間人數=總人數,(2)先由比例式可以得出抽調后的各車間人數,可知丙車間人數是由甲乙兩車間抽調過來組成的,因此可以設甲車間抽調了x人則乙車間抽調了35-x人,再根據甲車間人數比乙車間人數的4倍少5人列出方程求解.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,把一張矩形紙片ABCD沿EF折疊后,點A落在CD邊上的點A′處,點B落在點B′處,若∠2=40°,則圖中∠1的度數為( )

A. 115° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O(0,0),B(0,1)是正方形OBB1C的兩個頂點,以它的對角線OB1為一邊作正方形OB1B2C1 , 以正方形OB1B2C1的對角線OB2為一邊作正方形OB2B3C2 , 再以正方形OB2B3C2的對角線OB3為一邊作正方形OB3B4C3 , …,依次進行下去,則點B6的坐標是 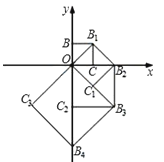
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國南宋時期杰出的數學家楊輝是錢塘人,下面的圖表是他在《詳解九章算術》中記載的“楊輝三角”.此圖揭示了 ![]() (
( ![]() 為非負整數)的展開式的項數及各項系數的有關規律.
為非負整數)的展開式的項數及各項系數的有關規律.

(1)請仔細觀察,填出(a+b)4的展開式中所缺的系數.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(2)此規律還可以解決實際問題:假如今天是星期三,再過7天還是星期三,那么再過 ![]() 天是星期 .
天是星期 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查適合采用抽樣調查的是( )
A. 某公司招聘人員,對應聘人員進行面試
B. 調查一批節能燈泡的使用壽命
C. 為保證火箭的成功發射,對其零部件進行檢查
D. 對乘坐某次航班的乘客進行安全檢查
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com