
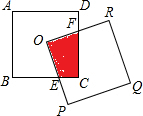
 如圖,兩個邊長都是2的正方形,其中正方形OPQR的頂點O是正方形ABCD的中心,有以下結論:
如圖,兩個邊長都是2的正方形,其中正方形OPQR的頂點O是正方形ABCD的中心,有以下結論: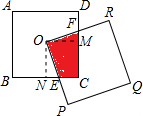 解:過正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,則四邊形OMCN是正方形,△OEM≌△OFN.
解:過正方形ABCD的中心O作OM⊥CD于M,作ON⊥BC于N,則四邊形OMCN是正方形,△OEM≌△OFN.

 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
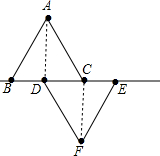 上,連接AD及CF.
上,連接AD及CF.查看答案和解析>>
科目:初中數學 來源: 題型:
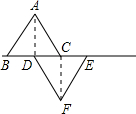 上,連接AD、CF.若BD=3cm,△ABC沿著BE的方向以每秒1cm的速度運動,設△ABC運動時間為t秒,
上,連接AD、CF.若BD=3cm,△ABC沿著BE的方向以每秒1cm的速度運動,設△ABC運動時間為t秒,查看答案和解析>>
科目:初中數學 來源: 題型:
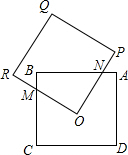 如圖所示,兩個邊長都為2的正方形ABCD和OPQR,如果O點正好是正方形ABCD的中心,而正方形OPQR可以繞O點旋轉,那么它們重疊部分的面積為( )
如圖所示,兩個邊長都為2的正方形ABCD和OPQR,如果O點正好是正方形ABCD的中心,而正方形OPQR可以繞O點旋轉,那么它們重疊部分的面積為( )| A、4 | ||
| B、2 | ||
| C、1 | ||
D、
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,兩個邊長都是2的正方形,其中正方形OPQR的頂點O是正方形ABCD的中心,有以下結論:
如圖,兩個邊長都是2的正方形,其中正方形OPQR的頂點O是正方形ABCD的中心,有以下結論:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com