
 如圖,在Rt△ABC中∠ACB=90°,CD⊥AB于D
如圖,在Rt△ABC中∠ACB=90°,CD⊥AB于D分析 (1)利用等角的余角相等得到∠B=∠ACD,則利用有兩組角對應相等的兩三角形相似可判斷△ADC∽△CDB;
(2)利用相似比得到$\frac{AD}{CD}$=$\frac{CD}{BD}$,然后利用比例性質求CD.
解答 (1)證明:∵CD⊥AB于D,
∴∠CDA=∠CDB=90°,
∴∠BCD+∠B=90°
∵∠ACB=90°,即∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△ADC∽△CDB;
(2)解:∵△ADC∽△CDB,
∴$\frac{AD}{CD}$=$\frac{CD}{BD}$,即$\frac{2}{CD}$=$\frac{CD}{6}$,
∴CD=2$\sqrt{3}$.
點評 本題考查了相似三角形的判定與性質:在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用;再運用相似三角形的性質時主要利用相似比進行幾何計算.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 垂線段就是垂直于已知直線的線段 | |
| B. | 垂線段就是垂直于已知直線并且與已知直線相交的線段 | |
| C. | 垂線段是一條豎起來的線段 | |
| D. | 過直線外一點向該直線作垂線,這一點到垂足之間的線段叫垂線段 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
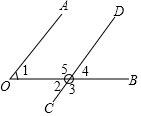 如圖,直線CD與∠AOB的邊OB相交.
如圖,直線CD與∠AOB的邊OB相交.查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:填空題
在平面直角坐標系中,點O為坐標原點,A、B、C三點的坐標為( ,0)、(3
,0)、(3 ,0)、(0,5),點D在第一象限,且∠ADB=60º,則線段CD的長的最小值為______.
,0)、(0,5),點D在第一象限,且∠ADB=60º,則線段CD的長的最小值為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com