
如圖,直線AB交x軸正半軸于點A(a,0),交y軸正半軸于點B(0,b),且a、b滿足  。
。

(1)求A、B兩點的坐標;
(2)D為OA的中點,連接BD,過點O作OE⊥ BD于 F,交AB于E,求證∠BDO=∠EDA;
(3)如圖,P為x軸上A點右側任意一點,以BP為邊作等腰Rt△PBM,其中PB=PM,直線MA交y軸于點Q,當點P在x軸上運動時,線段OQ的長是否發生變化?若不變,求其值;若變化,求線段OQ的取值范圍.
(1)A(4,0),B(0,4);(2)證明見解析;(3)無論P點怎么動OQ的長不變.
【解析】
試題分析:①首先根據已知條件和非負數的性質得到關于a、b的方程,解方程組即可求出a,b的值,也就能寫出A,B的坐標;
②作出∠AOB的平分線,通過證△BOG≌△OAE得到其對應角相等解決問題;
③過M作x軸的垂線,通過證明△PBO≌△MPN得出MN=AN,轉化到等腰直角三角形中去就很好解決了.
試題解析:①∵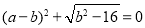
∴a=4,b=4,
∴A(4,0),B(0,4);
(2)證:作∠AOB的角平分線,交BD于G,
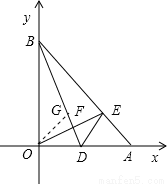
∴∠BOG=∠OAE=45°,OB=OA,
∠OBG=∠AOE=90°-∠BOF,
∴△BOG≌△OAE,
∴OG=AE.
∵∠GOD=∠EAD=45°,OD=AD,
∴△GOD≌△EDA.
∴∠GDO=∠ADE.
(3)過M作MN⊥x軸,垂足為N.
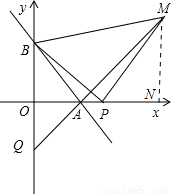
∵∠BPM=90°,
∴∠BPO+∠MPN=90°.
∵∠AOB=∠MNP=90°,
∴∠BPO=∠PMN,∠PBO=∠MPN.
∵BP=MP,
∴△PBO≌△MPN,
MN=OP,PN=AO=BO,
OP=OA+AP=PN+AP=AN,
∴MN=AN,∠MAN=45°.
∵∠BAO=45°,
∴∠BAO+∠OAQ=90°
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴無論P點怎么動OQ的長不變.
考點:1.全等三角形的判定與性質;2.非負數的性質:絕對值;3.非負數的性質:算術平方根.


科目:初中數學 來源:2014-2015學年江蘇東臺許河鎮中學八年級上學期第二次月檢數學試卷(解析版) 題型:選擇題
在 、
、 、
、 、
、 、
、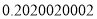 ……這六個數中,無理數有( ).
……這六個數中,無理數有( ).
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市八年級上學期期末考試數學試卷(解析版) 題型:選擇題
數軸上的點表示的數一定是( ).
A.有理數 B.無理數 C.實數 D.整數或有限小數
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省黃石市八年級9月月考數學試卷(解析版) 題型:解答題
已知:如圖所示,△ABC中,AB=AC,點E在CA的延長線上,且∠AEF=AFE,求證:EF⊥BC。
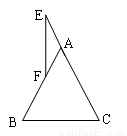
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省黃石市八年級9月月考數學試卷(解析版) 題型:填空題
四邊形ABCD中∠A、∠B、∠C、∠D的外角之比為1∶2∶3∶4,那么∠A∶∠B∶∠C∶∠D=________
查看答案和解析>>
科目:初中數學 來源:2014-2015學年貴州省安順市七年級上學期期末檢測數學試卷(解析版) 題型:計算題
計算:(每小題5分,共10分)
① 11-8÷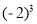 +3×(-2)
+3×(-2)
②-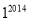 -6÷(-2)×
-6÷(-2)×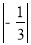
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com