
【題目】在ΔABC中,∠ABC的平分線與在∠ACE的平分線相交于點D.
(1)若∠ABC=60°,∠ACB=40°,求∠A和∠D的度數.
(2)由(1)小題的計算結果,猜想,∠A和∠D有什么數量關系,并加以證明.

【答案】答案見解析
【解析】試題分析:(1)根據三角形內角和定理和角平分線的性質,已知∠ABC=60°,∠ACB=40°,易求∠A和∠D度數.(2)根據三角形外角的性質以及角平分線性質,可得∠ACE=2∠D+∠ABC,∠ACE=∠A+∠ABC,即可得∠A和∠D的數量關系.
試題解析:解:(1)∵∠ABC=60°,∠ACB=40°,∴∠A=80°.
∵BD平分∠ABC,∠ABC=60°,
∴∠DBC=30°.
又∵∠ACB=40°,
∴∠ACE=140°.
又∵CD是∠ACE的平分線,
∴∠DCE=70°.
∴∠D=40°
(2)∠A=2∠D.
證明:∵CD 平分∠ACE
∴∠ACE=2∠DCE
又∠DCE=∠D+∠DBC
∴2∠DCE=2∠D+2∠DBC
∵BD平分∠ABC
∴∠ABC=2∠DBC
即∠ACE=2∠D+∠ABC
而∠ACE=∠A+∠ABC
∴2∠D=∠A


科目:初中數學 來源: 題型:
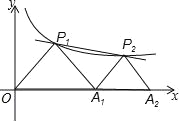
【題目】如圖,P1、P2是反比例函數![]() (k>0)在第一象限圖象上的兩點,點A1的坐標為(4,0).若△P1OA1與△P2A1A2均為等腰直角三角形,其中點P1、P2為直角頂點.
(k>0)在第一象限圖象上的兩點,點A1的坐標為(4,0).若△P1OA1與△P2A1A2均為等腰直角三角形,其中點P1、P2為直角頂點.
(1)求反比例函數的解析式.
(2)①求P2的坐標.
②根據圖象直接寫出在第一象限內當x滿足什么條件時,經過點P1、P2的一次函數的函數值大于反比例函數![]() 的函數值.
的函數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖A在數軸上所對應的數為﹣2.
(1)點B在點A右邊距A點4個單位長度,求點B所對應的數;
(2)在(1)的條件下,點A以每秒2個單位長度沿數軸向左運動,點 B 以每秒2個單位長度沿數軸向右運動,當點A運動到﹣6所在的點處時,求A,B兩點間距離.
(3)在(2)的條件下,現A點靜止不動,B點再以每秒2個單位長度沿數軸向左運動時,經過多長時間A,B兩點相距4個單位長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
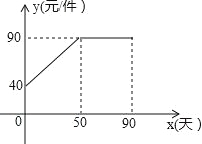
【題目】九年級(3)班數學興趣小組經過市場調查整理出某種商品在第x天(1≤x≤90,且x為整數)的售價與銷售量的相關信息如下.已知商品的進價為30元/件,設該商品的售價為y(單位:元/件),每天的銷售量為p(單位:件),每天的銷售利潤為w(單位:元).
時間x(天) | 1 | 30 | 60 | 90 |
每天銷售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w與x的函數關系式;
(2)問銷售該商品第幾天時,當天的銷售利潤最大?并求出最大利潤;
(3)該商品在銷售過程中,共有多少天每天的銷售利潤不低于5600元?請直接寫出結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從杭州東站到北京南站,原來最快的一趟高鐵G20次約用5h到達.從2018年4月10日起,全國鐵路開始實施新的列車運行圖,并啟用了“杭京高鐵復興號”,它的運行速度比原來的G20次的運行速度快35km/h,約用4.5h到達.如果在相同的路線上,杭州東站到北京南站的距離不變,設“杭京高鐵復興號”的運行速度為xkm/h,依題意,可列方程為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面坐標系內,點A位于第二象限,距離x軸1個單位長度,距離y軸4個單位長度,則點A的坐標為( )
A. (1,4) B. (﹣4,1) C. (﹣1,﹣4) D. (4,﹣1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com