Question

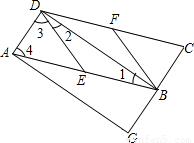
已知如圖在平行四邊形ABCD中，E、F分別為邊AB、CD的中點，BD是對角線，AG∥BD交CB的延長線于G.

（1）求證：△ADE≌△CBF；

（2）若四邊形BEDF是菱形，則四邊形AGBD是什么特殊四邊形？并證明你的結論。

 

Answer 1

【答案】

（1）證明：∵四邊形ABCD是平行四邊形，

∴∠4=∠C，AD=CB，AB=CD．

∵點E、F分別是AB、CD的中點，

∴AE=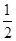AB，CF=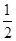CD．

∴AE=CF．

∴△ADE≌△CBF（SAS）．

（2）解：當四邊形BEDF是菱形時，四邊形AGBD是矩形．

證明：∵四邊形ABCD是平行四邊形，

∴AD∥BC．

∵AG∥BD，

∴四邊形AGBD是平行四邊形．

∵四邊形BEDF是菱形，

∴DE=BE．

∵AE=BE，

∴AE=BE=DE．

∴∠1=∠2，∠3=∠4．

∵∠1+∠2+∠3+∠4=180°，

∴2∠2+2∠3=180°．

∴∠2+∠3=90°．

即∠ADB=90°．

∴四邊形AGBD是矩形．

【解析】（1）在證明全等時常根據已知條件，分析還缺什么條件，然后用（SAS，ASA，SSS）來證明全等；

（2）先由菱形的性質得出AE=BE=DE，再通過角之間的關系求出∠2+∠3=90°即∠ADB=90°，所以判定四邊形AGBD是矩形．