
【題目】對于給定的![]() ,我們給出如下定義:若點M是邊
,我們給出如下定義:若點M是邊![]() 上的一個定點,且以M為圓心的半圓上的所有點都在
上的一個定點,且以M為圓心的半圓上的所有點都在![]() 的內部或邊上,則稱這樣的半圓為
的內部或邊上,則稱這樣的半圓為![]() 邊上的點M關于
邊上的點M關于![]() 的內半圓,并將半徑最大的內半圓稱為點M關于
的內半圓,并將半徑最大的內半圓稱為點M關于![]() 的最大內半圓.若點M是邊
的最大內半圓.若點M是邊![]() 上的一個動點(M不與B,C重合),則在所有的點M關于
上的一個動點(M不與B,C重合),則在所有的點M關于![]() 的最大內半圓中,將半徑最大的內半圓稱為
的最大內半圓中,將半徑最大的內半圓稱為![]() 關于
關于![]() 的內半圓.
的內半圓.
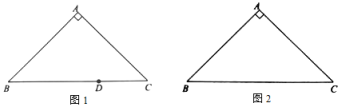
(1)在![]() 中,
中,![]() ,
,![]() ,
,
①如圖1,點D在邊![]() 上,且
上,且![]() ,直接寫出點D關于
,直接寫出點D關于![]() 的最大內半圓的半徑長;
的最大內半圓的半徑長;
②如圖2,畫出![]() 關于
關于![]() 的內半圓,并直接寫出它的半徑長;
的內半圓,并直接寫出它的半徑長;
(2)在平面直角坐標系![]() 中,點E的坐標為
中,點E的坐標為![]() ,點P在直線
,點P在直線![]() 上運動(P不與O重合),將
上運動(P不與O重合),將![]() 關于
關于![]() 的內半圓半徑記為R,當
的內半圓半徑記為R,當![]() 時,求點P的橫坐標t的取值范圍.
時,求點P的橫坐標t的取值范圍.
【答案】(1)①![]() ,②1,作圖見詳解;(2)t≥
,②1,作圖見詳解;(2)t≥![]() 或
或![]() .
.
【解析】
(1)①過點D作DE⊥AC,則以點D為圓心,DE長為半徑的半圓與AC相切,利用等腰直角三角形的性質,即可求解;
②當點D為BC的中點時,以D為圓心,DE為半徑的半圓就是![]() 關于
關于![]() 的內半圓,進而可求解;
的內半圓,進而可求解;
(2)設點P坐標為(t,![]() ),分兩種情況分類討論,①點P在第一象限時,②點P在第三象限時,分別求出t的取值范圍,即可.
),分兩種情況分類討論,①點P在第一象限時,②點P在第三象限時,分別求出t的取值范圍,即可.
(1)①如圖1,過點D作DE⊥AC,則以點D為圓心,DE長為半徑的半圓與AC相切,
∴D關于![]() 的最大內半圓的半徑長就是DE的長,
的最大內半圓的半徑長就是DE的長,
∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴DE=CD÷![]() =1÷
=1÷![]() =
=![]()
②如圖2,當點D為BC的中點時,以D為圓心,DE為半徑的半圓就是![]() 關于
關于![]() 的內半圓,
的內半圓,
∵在![]() 中,
中,![]() ,
,![]() ,DE⊥AC ,
,DE⊥AC ,
∴DE∥BA,
∴DE=![]() =
=![]() ×2=1;
×2=1;
(2)∵點P在直線![]() 上,
上,
∴∠POE=30°
設點P坐標為(t,![]() ),
),
∵點E的坐標為![]() ,
,
∴OE=3,
①若點P在第一象限時,設點M是線段OE上的動點,作MN⊥OP,MG⊥PE,
∵![]() ,
,
∴當R=![]() 時,如圖3,則MN=MG=
時,如圖3,則MN=MG=![]() ,OM=2×MN==2×
,OM=2×MN==2×![]() =
=![]() ,
,
∴ME=3-![]() =
=![]() ,
,
∴OM=ME,
在RtOMN和RtEMG中,
∵![]()
∴RtOMN RtEMG(HL)
∴∠MON=∠MEG=30°,
∴點P的橫坐標t=![]() ,
,
當R=1時,如圖4,則MN=1,OM=2×MN==2×1=2,此時,點P的橫坐標t≥3,
∴t≥![]() 時,
時,![]() ;
;
②若點P在第三象限時,作 MG⊥PE,PH⊥x軸,
當R=![]() 時,如圖5,則MG=MO=
時,如圖5,則MG=MO=![]() ,
,
∴ME=3-MO=3-![]() =
=![]() ,
,
∴EG=![]() ,
,
∴tanE=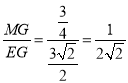 ,
,
∴![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴![]() 時,
時,![]() .
.
綜上所述:t≥![]() 或
或![]() .
.
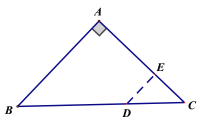
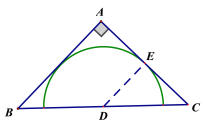
圖1 圖2
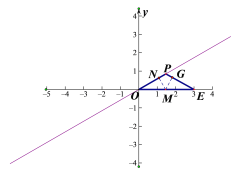

圖3 圖4
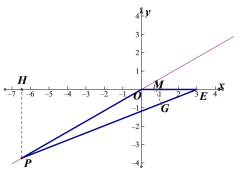
圖5


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長是3,BP=CQ,連接AQ,DP交于點O,并分別與邊CD,BC交于點F,E,連接AE,下列結論:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四邊形OECF;④當BP=1時,tan∠OAE=![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情防控,我們一直在堅守.某居委會組織兩個檢查組,分別對“居民體溫”和“居民安全出行”的情況進行抽查.若這兩個檢查組在轄區內的某三個校區中各自隨機抽取一個小區進行檢查,則他們恰好抽到同一個小區的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:連結菱形的一邊中點與對邊的兩端點的線段把它分成三個三角形,如果其中有兩個三角形相似,那么稱這樣的菱形為自相似菱形.
(1)判斷下列命題是真命題,還是假命題?
①正方形是自相似菱形;
②有一個內角為60°的菱形是自相似菱形.
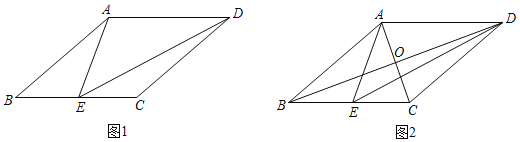
③如圖1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E為BC中點,則在△ABE,△AED,△EDC中,相似的三角形只有△ABE與△AED.
(2)如圖2,菱形ABCD是自相似菱形,∠ABC是銳角,邊長為4,E為BC中點.
①求AE,DE的長;
②AC,BD交于點O,求tan∠DBC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數![]() 的圖象G經過點
的圖象G經過點![]() ,直線
,直線![]() 與y軸交于點B,與圖象G交于點C.
與y軸交于點B,與圖象G交于點C.
(1)求m的值.
(2)橫、縱坐標都是整數的點叫做整點.記圖象G在點A,C之間的部分與線段BA,BC圍成的區域(不含邊界)為W.
①當直線l過點![]() 時,直接寫出區域W內的整點個數.
時,直接寫出區域W內的整點個數.
②若區域W內的整點不少于4個,結合函數圖象,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,當m,n滿足mn=k(k為常數,且m>0,n>0)時,就稱點(m,n)為“等積點”.若直線y=﹣x+b(b>0)與x軸、y軸分別交于點A和點B,并且該直線上有且只有一個“等積點”,過點A與y軸平行的直線和過點B與x軸平行的直線交于點C,點E是直線AC上的“等積點”,點F是直線BC上的“等積點”,若△OEF的面積為![]() ,則OE=______.
,則OE=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
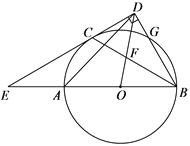
【題目】如圖,AB是⊙O的直徑,C,G是⊙O上兩點,且![]() ,過點C的直線CD⊥BG于點D,交BA的延長線于點E,連接BC,交OD于點F.
,過點C的直線CD⊥BG于點D,交BA的延長線于點E,連接BC,交OD于點F.
(1)求證:CD是⊙O的切線;
(2)若![]() ,求證:AE=AO;
,求證:AE=AO;
(3)連接 AD,在(2)的條件下,若CD ![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】青山區政府美化城市環境,計劃對面積為![]() 平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的
平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的![]() 倍,并且在獨立完成面積為平
倍,并且在獨立完成面積為平![]() 方米區域的綠化時,甲隊比乙隊多用
方米區域的綠化時,甲隊比乙隊多用![]() 天.
天.
![]() 求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
![]() 若區政府每天需付給甲隊的綠化費用為
若區政府每天需付給甲隊的綠化費用為![]() 萬元,乙隊為
萬元,乙隊為![]() 萬元,要使這次的綠化總費用不超過
萬元,要使這次的綠化總費用不超過![]() 萬元,至少應安排甲隊工作多少天?
萬元,至少應安排甲隊工作多少天?
![]() 為合理利用綠化用地,這是需要用長為
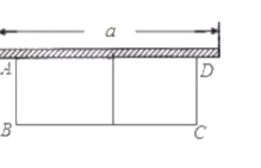
為合理利用綠化用地,這是需要用長為![]() 米的植物隔離帶靠著墻(墻的最大可用長度為
米的植物隔離帶靠著墻(墻的最大可用長度為![]() 是
是![]() 米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬
米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬![]() 為
為![]() 米,面積為
米,面積為![]() 米
米![]() .試問中央綠地的面積能達到
.試問中央綠地的面積能達到![]() 嗎?如果能,請求出此時
嗎?如果能,請求出此時![]() 的長;如果不能,請說明理由.
的長;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水產品養殖企業為指導該企業某種產品的養殖和銷售,對歷年市場行情和水產品的養殖情況進行了調查.調查發現這種水產品的每千克售價![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足關系式
(月)滿足關系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足的函數關系如圖所示:
(月)滿足的函數關系如圖所示:
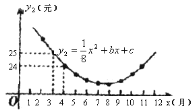
(1)試確定![]() 、
、![]() 的值;
的值;
(2)求出這種水產品每千克的利潤![]() (元)與銷售月份
(元)與銷售月份![]() (月)之間的函數關系式;
(月)之間的函數關系式;
(3)幾月份出售這種水產品每千克利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com