
【題目】如圖1,已知拋物線y=![]() x2﹣
x2﹣![]() x﹣3與x軸交于A和B兩點(點A在點B的左側),與y軸相交于點C,頂點為D
x﹣3與x軸交于A和B兩點(點A在點B的左側),與y軸相交于點C,頂點為D

(1)求出點A,B,D的坐標;
(2)如圖1,若線段OB在x軸上移動,且點O,B移動后的對應點為O′,B′.首尾順次連接點O′、B′、D、C構成四邊形O′B′DC,請求出四邊形O′B′DC的周長最小值.
(3)如圖2,若點M是拋物線上一點,點N在y軸上,連接CM、MN.當△CMN是以MN為直角邊的等腰直角三角形時,直接寫出點N的坐標.
【答案】(1)A(﹣2,0),B(4,0),D(1,﹣![]() );(2)4+
);(2)4+![]() +
+![]() ;(3)N的坐標為(0,
;(3)N的坐標為(0,![]() )、(0,
)、(0,![]() )、(0,﹣
)、(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
試題分析:(1)令拋物線解析式中y=0,解關于x的一元二次方程即可求出點A、B的坐標,再利用配方法將拋物線解析式進行配方即可得出頂點D的坐標;(2)作點C(0,﹣3)關于x軸的對稱點C′(0,3),將點C′(0,3)向右平移4個單位得到點C″(4,3),連接DC″,交x軸于點B′,將點B′向左平移4個單位得到點O′,連接CO′,CO″,則四邊形O′B′C′C″為平行四邊形,此時四邊形O′B′DC周長取最小值.再根據兩點間的距離公式求出CD、DC″的長度,即可得出結論;(3)按點M的位置不同分兩種情況考慮:①點M在直線y=x﹣3上,聯立直線與拋物線解析式求出點M的坐標,結合點C的坐標以及等腰直角三角形的性質即可得出點N的坐標;②點M在直線y=﹣x﹣3上,聯立直線與拋物線解析式求出點M的坐標,結合點C的坐標以及等腰直角三角形的性質即可得出點N的坐標.綜合兩種情況即可得出結論.
試題解析:(1)令y=![]() x2﹣
x2﹣![]() x﹣3中y=0,則
x﹣3中y=0,則![]() x2﹣
x2﹣![]() x﹣3=0,解得:x1=﹣2,x2=4,∴A(﹣2,0),B(4,0).∵y=
x﹣3=0,解得:x1=﹣2,x2=4,∴A(﹣2,0),B(4,0).∵y=![]() x2﹣
x2﹣![]() x﹣3=
x﹣3=![]() (x2﹣2x)﹣3=
(x2﹣2x)﹣3=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,∴D(1,﹣
,∴D(1,﹣![]() ).(2)令y=
).(2)令y=![]() x2﹣
x2﹣![]() x﹣3中x=0,則y=﹣3,∴C(0,﹣3).D(1,﹣
x﹣3中x=0,則y=﹣3,∴C(0,﹣3).D(1,﹣![]() ),O′B′=OB=4.如圖1,
),O′B′=OB=4.如圖1,
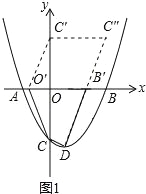
作點C(0,﹣3)關于x軸的對稱點C′(0,3),將點C′(0,3)向右平移4個單位得到點C″(4,3),連接DC″,交x軸于點B′,將點B′向左平移4個單位得到點O′,連接CO′,C′O′,則四邊形O′B′C′C″為平行四邊形,此時四邊形O′B′DC周長取最小值.此時C四邊形O′B′DC=CD+O′B′+CO′+DB′=CD+O′B′+DC″.∵O′B′=4,CD=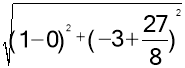 =
=![]() ,C″D=
,C″D=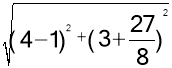 =
=![]() ,∴四邊形O′B′DC的周長最小值為4+
,∴四邊形O′B′DC的周長最小值為4+![]() +
+![]() .(3)△CMN是以MN為直角邊的等腰直角三角形分兩種情況(如圖2):
.(3)△CMN是以MN為直角邊的等腰直角三角形分兩種情況(如圖2):
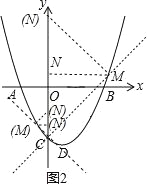 ,①過點C作直線y=x﹣3交拋物線于點M,聯立直線CM和拋物線的解析式得:
,①過點C作直線y=x﹣3交拋物線于點M,聯立直線CM和拋物線的解析式得: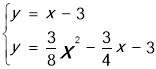 ,解得:
,解得: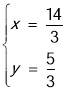 或
或![]() (舍去),∴M(
(舍去),∴M(![]() ,
,![]() ).∵△CMN為等腰直角三角形,C(0,﹣3),∴點N的坐標為(0,
).∵△CMN為等腰直角三角形,C(0,﹣3),∴點N的坐標為(0,![]() )或(0,
)或(0,![]() );②過點C作直線y=﹣x﹣3交拋物線于點M,聯立直線CM和拋物線的解析式得:
);②過點C作直線y=﹣x﹣3交拋物線于點M,聯立直線CM和拋物線的解析式得: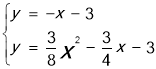 ,解得:
,解得: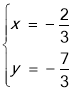 或
或![]() (舍去),∴M(﹣
(舍去),∴M(﹣![]() ,﹣
,﹣![]() ).∵△CMN為等腰直角三角形,C(0,﹣3),∴點N的坐標為(0,﹣
).∵△CMN為等腰直角三角形,C(0,﹣3),∴點N的坐標為(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ).綜上可知:當△CMN是以MN為直角邊的等腰直角三角形時,點N的坐標為(0,
).綜上可知:當△CMN是以MN為直角邊的等腰直角三角形時,點N的坐標為(0,![]() )、(0,
)、(0,![]() )、(0,﹣
)、(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ).
).


科目:初中數學 來源: 題型:
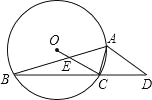
【題目】如圖所示,⊙O的內接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延長線于D點,OC交AB于E點.
(1)求∠D的度數;
(2)求證:AC2=ADCE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今夏,十堰市王家河村瓜果喜獲豐收,果農王二胖收獲西瓜20噸,香瓜12噸,現計劃租用甲、乙兩種貨車共8輛將這批瓜果全部運往外地銷售,已知一輛甲種貨車可裝西瓜4噸和香瓜1噸,一輛乙種貨車可裝西瓜和香瓜各2噸.
(1)果農王二胖如何安排甲、乙兩種貨車可一次性地運到銷售地?有幾種方案?
(2)若甲種貨車每輛要付運輸費300元,乙種貨車每輛要付運輸費240元,則果農王二胖應選擇哪種方案,使運輸費最少?最少運費是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一張圓心角為108°,半徑為4cm的扇形紙片,小紅剪去圓心角為θ的部分扇形紙片后,將剩下的紙片制作成一個底面半徑為1cm的圓錐形紙帽(接縫處不重疊),則剪去的扇形紙片的面積為( ).
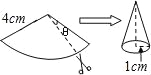
A.0.8πcm2 B.3.2πcm2 C.4πcm2 D.4.8πcm2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com