
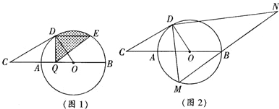
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 切
切![]() 于點
于點![]() ,
,![]() ,
,![]() 是
是![]() 半徑的
半徑的![]() 倍.
倍.
![]() 求
求![]() 的半徑
的半徑![]() ;
;
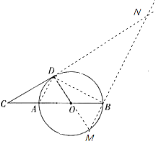
![]() 如圖
如圖![]() ,弦
,弦![]() ,動點
,動點![]() 從
從![]() 出發沿直徑
出發沿直徑![]() 向
向![]() 運動的過程中,圖中陰影部分的面積是否發生變化,若發生變化,請你說明理由;若不發生變化,請你求出陰影部分的面積;
運動的過程中,圖中陰影部分的面積是否發生變化,若發生變化,請你說明理由;若不發生變化,請你求出陰影部分的面積;
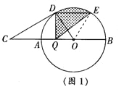
![]() 如圖
如圖![]() ,動點
,動點![]() 從
從![]() 出發,在
出發,在![]() 上按逆時針方向向
上按逆時針方向向![]() 運動.連接
運動.連接![]() ,過
,過![]() 作
作![]() 的垂線,與
的垂線,與![]() 的延長線交于點
的延長線交于點![]() ,當點
,當點![]() 運動到什么位置時,
運動到什么位置時,![]() 取到最大值?求此時動點
取到最大值?求此時動點![]() 所經過的弧長.
所經過的弧長.
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意,CD是⊙O半徑的![]() 倍,CA=1,在直角△CDO中,根據勾股定理CD2+OD2=CO2,代入即可求出;
倍,CA=1,在直角△CDO中,根據勾股定理CD2+OD2=CO2,代入即可求出;
(2)由DE∥CB,可知,動點Q從A出發沿直徑AB向B運動的過程中,△DEQ的面積不變,則陰影部分的面積不變;當點Q運動到O點時,則∠DOE=60°,即可求出陰影部分的面積;
(3)如圖,連接AD、BD,當DM過圓心O時,DN取到最大值;易證△ADB∽△MDN,由已知,可求得,AD=1,BD=![]() ,所以,DN=
,所以,DN=![]() DM,此時,∠AOM=120°,即可求得
DM,此時,∠AOM=120°,即可求得![]() 的長.
的長.
解:![]() ∵
∵![]() 切
切![]() 于點
于點![]() ,
,
∴三角形![]() 是直角三角形,
是直角三角形,
∵![]() ,
,![]() 是
是![]() 半徑的
半徑的![]() 倍,
倍,
∴在直角![]() 中,
中,![]() ,
,
則,![]() ,
,
∴![]() ;
;
![]() ∵
∵![]() ,
,
∴動點![]() 從
從![]() 出發沿直徑
出發沿直徑![]() 向
向![]() 運動的過程中,
運動的過程中,![]() 的底
的底![]() 不變,底
不變,底![]() 上的高不變,
上的高不變,
∴![]() 的面積不變,則陰影部分的面積不變;
的面積不變,則陰影部分的面積不變;
由![]() ,
,![]() ,
,
∴![]() ,則
,則![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ;
;
![]() 如圖,連接
如圖,連接![]() 、
、![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴當![]() 為最大值,即
為最大值,即![]() 過圓心
過圓心![]() 時,
時,![]() 取到最大值;
取到最大值;
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.


 名師點撥卷系列答案
名師點撥卷系列答案科目:初中數學 來源: 題型:
【題目】對于二次函數![]() .
.
![]() 它的圖象與二次函數
它的圖象與二次函數![]() 的圖象有什么關系?它是軸對稱圖形嗎?它的開口方向,對稱軸和頂點坐標分別是什么?
的圖象有什么關系?它是軸對稱圖形嗎?它的開口方向,對稱軸和頂點坐標分別是什么?
![]() 當
當![]() 取哪些值時,
取哪些值時,![]() 的值隨
的值隨![]() 的增大而增大?當
的增大而增大?當![]() 取哪些值時,
取哪些值時,![]() 的值隨
的值隨![]() 的增大而減小?
的增大而減小?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某農場老板準備建造一個矩形羊圈![]() ,他打算讓矩形羊圈的一面完全靠著墻
,他打算讓矩形羊圈的一面完全靠著墻![]() ,墻
,墻![]() 可利用的長度為
可利用的長度為![]() ,另外三面用長度為
,另外三面用長度為![]() 的籬笆圍成(籬笆正好要全部用完,且不考慮接頭的部分)
的籬笆圍成(籬笆正好要全部用完,且不考慮接頭的部分)

![]() 若要使矩形羊圈的面積為
若要使矩形羊圈的面積為![]() ,則垂直于墻的一邊長
,則垂直于墻的一邊長![]() 為多少米?
為多少米?
![]() 農場老板又想將羊圈
農場老板又想將羊圈![]() 的面積重新建造成面積為
的面積重新建造成面積為![]() ,從而可以養更多的羊,請聰明的你告訴他:他的這個想法能實現嗎?為什么?
,從而可以養更多的羊,請聰明的你告訴他:他的這個想法能實現嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】科技創新加速中國高鐵技術發展,某建筑集團承擔一座高架橋的鋪設任務,在合同期內高效完成了任務,這是記者與該集團工程師的一段對話:
記者:你們是用9天完成4800米長的高架橋鋪設任務的?
工程師:是的,我們鋪設600米后,采用新的鋪設技術,這樣每天鋪設長度是原來的2倍.
通過這段對話,請你求出該建筑集團原來每天鋪設高架橋的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場將進價為2000元的冰箱以2400元售出,平均每天能售出8臺,為了配合國家“家電下鄉”政策的實施,商場決定采取適當的降價措施.調查表明:這種冰箱的售價每降低50元,平均每天就能多售出 4臺.商場要想在這種冰箱銷售中每天盈利 4800 元,同時又要使百姓得到實惠,每臺冰箱應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() ,
,![]() .
.
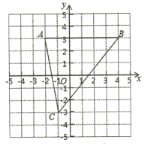
(1)點![]() 到
到![]() 軸的距離為:______;
軸的距離為:______;
(2)![]() 的三邊長為:
的三邊長為:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)當點![]() 在
在![]() 軸上,且
軸上,且![]() 的面積為6時,點
的面積為6時,點![]() 的坐標為:______.
的坐標為:______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() 的圖像為直線
的圖像為直線![]() .
.
(1)若直線![]() 與正比例函數
與正比例函數![]() 的圖像平行,且過點(0,2),求直線
的圖像平行,且過點(0,2),求直線![]() 的函數表達式;
的函數表達式;
(2)若直線![]() 過點(3,0),且與兩坐標軸圍成的三角形面積等于3,求
過點(3,0),且與兩坐標軸圍成的三角形面積等于3,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com