
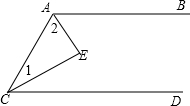
 如圖,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E為多少?
如圖,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E為多少? ∠ACD (原因:________)
∠ACD (原因:________) ∠CAB(原因:________)
∠CAB(原因:________) (∠CAB+∠ACD)=90°(等量代換)
(∠CAB+∠ACD)=90°(等量代換) ∠ACD,∠2=∠BAE=
∠ACD,∠2=∠BAE= ∠CAB,再根據平行線的性質得出∠CAB+∠ACD=180°,利用三角形內角和定理即可得出答案.
∠CAB,再根據平行線的性質得出∠CAB+∠ACD=180°,利用三角形內角和定理即可得出答案. ∠ACD (角平分線的定義),
∠ACD (角平分線的定義), ∠CAB(原因:角平分線的定義),
∠CAB(原因:角平分線的定義), (∠CAB+∠ACD)=90°(等量代換),
(∠CAB+∠ACD)=90°(等量代換),

 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com