
如圖,已知二次函數 =
= ,當
,當 <
< <
< 時,
時,  隨
隨 的增大而增大,則實數a的取值范圍是 ( )
的增大而增大,則實數a的取值范圍是 ( )
A. > > | B. < < ≤ ≤ | C. >0 >0 | D. < < < < |
 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:解答題
青海新聞網訊:西寧市為加大向國家環境保護模范城市大步邁進的步伐,積極推進城市綠地、主題公園、休閑場地建設.園林局利用甲種花卉和乙種花卉搭配成A、B兩種園藝造型擺放在夏都大道兩側.搭配數量如下表所示:
| | 甲種花卉(盆) | 乙種花卉(盆) |
| A種園藝造型(個) |  盆 盆 |  盆 盆 |
| B種園藝造型(個) |  盆 盆 |  盆 盆 |
 元.若園林局搭配A種園藝造型
元.若園林局搭配A種園藝造型 個,B種園藝造型
個,B種園藝造型 個共投入
個共投入 元.則A、B兩種園藝 造型的單價分別是多少元?
元.則A、B兩種園藝 造型的單價分別是多少元? 個,某校學生課外小組承接了搭配方案的設計,其中甲種花卉不超過
個,某校學生課外小組承接了搭配方案的設計,其中甲種花卉不超過 盆,乙種花卉不超過
盆,乙種花卉不超過 盆,問符合題意的搭配方案有幾種?請你幫忙設計出來.
盆,問符合題意的搭配方案有幾種?請你幫忙設計出來.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,直線AB分別與x軸,y軸相交于A,B兩點,OA,OB的長分別是方程x2﹣14x+48=0的兩根,且OA<OB.
(1)求點A,B的坐標.
(2)過點A作直線AC交y軸于點C,∠1是直線AC與x軸相交所成的銳角,sin∠1= ,點D在線段CA的延長線上,且AD=AB,若反比例函數
,點D在線段CA的延長線上,且AD=AB,若反比例函數 的圖象經過點D,求k的值.
的圖象經過點D,求k的值.
(3)在(2)的條件下,點M在射線AD上,平面內是否存在點N,使以A,B,M,N為頂點的四邊形是鄰邊之比為1:2的矩形?若存在,請直接寫出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知直線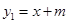 與
與 軸、
軸、 軸分別交于點
軸分別交于點 ,與雙曲線
,與雙曲線
 分別交于點
分別交于點 ,且
,且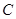 點的坐標為
點的坐標為 .
.
(1)分別求出直線 及雙曲線的解析式;
及雙曲線的解析式;
(2)求出點 的坐標;
的坐標;
(3)利用圖象直接寫出:當 在什么范圍內取值時,
在什么范圍內取值時,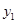 >
> .
.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知雙曲線 經過點D(6,1),點C是雙曲線第三象限分支上的動點,過C作CA⊥x軸,過D作DB⊥y軸,垂足分別為A,B,連接AB,BC.
經過點D(6,1),點C是雙曲線第三象限分支上的動點,過C作CA⊥x軸,過D作DB⊥y軸,垂足分別為A,B,連接AB,BC.
(1)求k的值;
(2)若△BCD的面積為12,求直線CD的解析式;
(3)判斷AB與CD的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
已知二次函數y=-x2+2bx+c,當x>1時,y的值隨x值的增大而減小,則實數b的取值范圍是( )
| A.b≥-1 | B.b≤-1 | C.b≥1 | D.b≤1 |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,在矩形ABCD中,AB=2cm,BC=4cm,對角線AC,BD相交于點O,點E,F分別從B,C兩點同時出發,以1cm/s的速度分別沿B→C,C→D運動,點F運動到點D時停止,點E運動到點C時停止.設運動時間為t(單位:s),△OEF的面積為S(單位:cm2),則S與t的函數關系可用圖象表示為( )
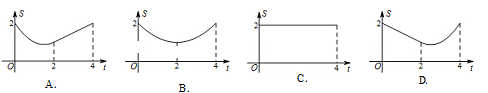
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
數形結合是數學中常用的思想方法,試運用這一思想方法確定函數y=x2+1與y= 的交點的橫坐標x0的取值范圍是( )
的交點的橫坐標x0的取值范圍是( )
| A.0<x0<1 |
| B.1<x0<2 |
| C.2<x0<3 |
| D.﹣1<x0<0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com