
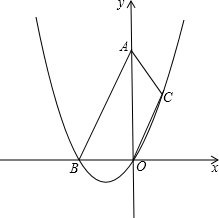
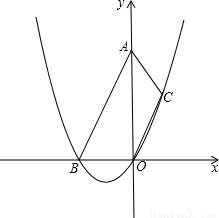
 已知等腰梯形ABOC在直角坐標系中如圖所示,AB∥OC,OB=2,OA=
已知等腰梯形ABOC在直角坐標系中如圖所示,AB∥OC,OB=2,OA= .
.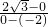 =
= ,
,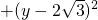 =22,①
=22,① x,②
x,② ,C點的坐標為(1,
,C點的坐標為(1, );
); )代入y=ax2+bx+c得方程組:
)代入y=ax2+bx+c得方程組: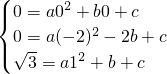 ,
, ,b=
,b= ,c=0,
,c=0,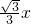 2+
2+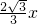 ;
; ),
),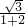 =
= ,
,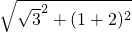 =2
=2 ,
, x+b,①
x+b,①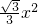 +
+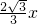 ,②
,②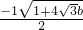 ;
;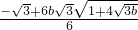 為P點的坐標,Q點的坐標為(0,b),
為P點的坐標,Q點的坐標為(0,b),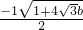 -0)+(=
-0)+(=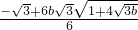 -b)2=12,
-b)2=12, 和b=4
和b=4 ,
, 時,x,=-3,y=
時,x,=-3,y= 或x=2,y=
或x=2,y= ,
, 時,x=-4,y=
時,x=-4,y= 或x=3,y=5
或x=3,y=5 ,
, ),P2(3,5
),P2(3,5 )符合題意要求,
)符合題意要求, x+2
x+2 ,
, x+4
x+4 ,
, ),Q2(0,4
),Q2(0,4 )可以構成兩個平行四邊形.
)可以構成兩個平行四邊形.

 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
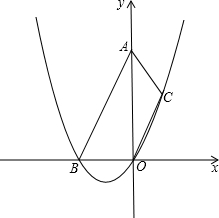 已知等腰梯形ABOC在直角坐標系中如圖所示,AB∥OC,OB=2,OA=2
已知等腰梯形ABOC在直角坐標系中如圖所示,AB∥OC,OB=2,OA=2| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2011年3月九年級(下)階段性測試數學試卷(解析版) 題型:解答題
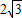 .
.
查看答案和解析>>
科目:初中數學 來源:2012年上海市寶山區金山區中考數學一模試卷(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com