
【題目】如圖,點P在⊙O的直徑AB的延長線上,PC為⊙O的切線,點C為切點,連接AC,過點A作PC的垂線,點D為垂足,AD交⊙O于點E.
(1)如圖1,求證:∠DAC=∠PAC;
(2)如圖2,點F(與點C位于直徑AB兩側)在⊙O上,![]() ,連接EF,過點F作AD的平行線交PC于點G,求證:FG=DE+DG;
,連接EF,過點F作AD的平行線交PC于點G,求證:FG=DE+DG;
(3)在(2)的條件下,如圖3,若AE=![]() DG,PO=5,求EF的長.
DG,PO=5,求EF的長.

【答案】(1)證明見解析;(2)證明見解析;(3)EF=3![]() .
.
【解析】
(1)連接OC,求出OC∥AD,求出OC⊥PC,根據切線的判定推出即可;
(2)連接BE交GF于H,連接OH,求出四邊形HGDE是矩形,求出DE=HG,FH=EH,即可得出答案;
(3)設OC交HE于M,連接OE、OF,求出∠FHO=∠EHO=45°,根據矩形的性質得出EH∥DG,求出OM=![]() AE,設OM=a,則HM=a,AE=2a,AE=
AE,設OM=a,則HM=a,AE=2a,AE=![]() DG,DG=3a,
DG,DG=3a,
求出ME=CD=2a,BM=2a,解直角三角形得出tan∠MBO=![]() ,tanP=
,tanP=![]() ,設OC=k,則PC=2k,根據OP=
,設OC=k,則PC=2k,根據OP=![]() k=5求出k=
k=5求出k=![]() ,根據勾股定理求出a,即可求出答案.
,根據勾股定理求出a,即可求出答案.
(1)證明:連接OC,
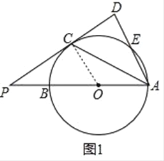
∵PC為⊙O的切線,
∴OC⊥PC,
∵AD⊥PC,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OC=OA,
∴∠PAC=∠OCA,
∴∠DAC=∠PAC;
(2)證明:連接BE交GF于H,連接OH,
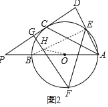
∵FG∥AD,
∴∠FGD+∠D=180°,
∵∠D=90°,
∴∠FGD=90°,
∵AB為⊙O的直徑,
∴∠BEA=90°,
∴∠BED=90°,
∴∠D=∠HGD=∠BED=90°,
∴四邊形HGDE是矩形,
∴DE=GH,DG=HE,∠GHE=90°,
∵![]() ,
,
∴∠HEF=∠FEA=![]() ∠BEA=
∠BEA=![]() =45°,
=45°,
∴∠HFE=90°﹣∠HEF=45°,
∴∠HEF=∠HFE,
∴FH=EH,
∴FG=FH+GH=DE+DG;
(3)解:設OC交HE于M,連接OE、OF,
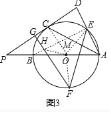
∵EH=HF,OE=OF,HO=HO,
∴△FHO≌△EHO,
∴∠FHO=∠EHO=45°,
∵四邊形GHED是矩形,
∴EH∥DG,
∴∠OMH=∠OCP=90°,
∴∠HOM=90°﹣∠OHM=90°﹣45°=45°,
∴∠HOM=∠OHM,
∴HM=MO,
∵OM⊥BE,
∴BM=ME,
∴OM=![]() AE,
AE,
設OM=a,則HM=a,AE=2a,AE=![]() DG,DG=3a,
DG,DG=3a,
∵∠HGC=∠GCM=∠GHE=90°,
∴四邊形GHMC是矩形,
∴GC=HM=a,DC=DG﹣GC=2a,
∵DG=HE,GC=HM,
∴ME=CD=2a,BM=2a,
在Rt△BOM中,tan∠MBO=![]() ,
,
∵EH∥DP,
∴∠P=∠MBO,
tanP=![]() ,
,
設OC=k,則PC=2k,
在Rt△POC中,OP=![]() k=5,
k=5,
解得:k=![]() ,OE=OC=
,OE=OC=![]() ,
,
在Rt△OME中,OM2+ME2=OE2,5a2=5,
a=1,
∴HE=3a=3,
在Rt△HFE中,∠HEF=45°,
∴EF=![]() HE=3
HE=3![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,從A地到B地的公路需要經過C地,根據規劃,將在A,B兩地之間修建一條筆直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的長(結果精確到0.1千米)
(參考數據:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=x2﹣(3m+1)x+2m2+m(m>0),與y軸交于點C,與x軸交于點A(x1,0),B(x2,0),且x1<x2.
(1)求2x1﹣x2+3的值;
(2)當m=2x1﹣x2+3時,將此拋物線沿對稱軸向上平移n個單位,使平移后得到的拋物線頂點落在△ABC的內部(不包括△ABC的邊),求n的取值范圍(直接寫出答案即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 為線段
為線段![]() 上一動點(不與點
上一動點(不與點![]() ,
,![]() 重合),在
重合),在![]() 同側分別作等邊
同側分別作等邊![]() 和等邊
和等邊![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() .下列五個結論:①
.下列五個結論:①![]() ;②
;②![]() ;③
;③![]() ;④DE=DP;⑤
;④DE=DP;⑤![]() .其中正確結論的個數是( )
.其中正確結論的個數是( )

A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,△ABC中,作∠ABC、∠ACB的平分線相交于點O,過點O作EF∥BC分別交AB、AC于E、F.
①求證:OE=BE.
②若△ABC的周長是25,BC=9,試求出△AEF的周長.
(2)如圖2,若∠ABC的平分線與∠ACB外角∠ACD的平分線相交于點P,連接AP,若∠BAC=80°,∠PAC的度數?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,F是CD上一點,E是BF上一點,連接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,則下列結論中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正確的個數有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,點A、B、C在x軸上,點D、E在y軸上,OA=OD=2,OC=OE=4,B為線段OA的中點,直線AD與經過B、E、C三點的拋物線交于F、G兩點,與其對稱軸交于M,點P為線段FG上一個動點(與F、G不重合),PQ∥y軸與拋物線交于點Q.
(1)求經過B、E、C三點的拋物線的解析式;
(2)判斷△BDC的形狀,并給出證明;當P在什么位置時,以P、O、C為頂點的三角形是等腰三角形,并求出此時點P的坐標;
(3)若拋物線的頂點為N,連接QN,探究四邊形PMNQ的形狀:①能否成為菱形;②能否成為等腰梯形?若能,請直接寫出點P的坐標;若不能,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com