
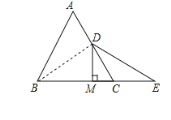
【題目】如圖,在等邊三角形![]() 中,
中,![]() 為
為![]() 邊的中點(diǎn),
邊的中點(diǎn),![]() 為
為![]() 邊的延長(zhǎng)線上一點(diǎn),
邊的延長(zhǎng)線上一點(diǎn),![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() .下列結(jié)論錯(cuò)誤的是( )
.下列結(jié)論錯(cuò)誤的是( )

A.![]()
B.![]()
C.![]()
D.![]() .
.
【答案】D
【解析】
根據(jù)等邊三角形的性質(zhì)得到∠ACB=∠ABC=60°,再由![]() 求得∠E=
求得∠E=![]() ∠ACB=30°然后依次對(duì)各選項(xiàng)判斷即可.
∠ACB=30°然后依次對(duì)各選項(xiàng)判斷即可.
解:∵△ABC是等邊△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E=![]() ∠ACB=30°,
∠ACB=30°,
連接BD,
∵等邊△ABC中,D是AC的中點(diǎn),
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∴∠DBC=∠E=30°,
∴DB=DE,
又∵DM⊥BC,
∴BM=EM,故B正確;
∵CM=![]() CD=
CD=![]() CE,故C正確,故D錯(cuò)誤;
CE,故C正確,故D錯(cuò)誤;
∴ME=3CM,
∴BM=3CM,故A正確;
故選:D.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】解下列各題:
(1)先化簡(jiǎn),再求代數(shù)式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是銳角,且sin(α+15°)=![]() .計(jì)算
.計(jì)算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】平面直角坐標(biāo)系中,A(0,3),B(4,0),C(﹣1,﹣1),點(diǎn) P 線段 AB上一動(dòng)點(diǎn),將線段 AB 繞原點(diǎn) O 旋轉(zhuǎn)一周,點(diǎn) P 的對(duì)應(yīng)點(diǎn)為 P′,則 P′C 的最大值為_____,最小值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,以AC為斜邊向外作等腰直角三角形COA,已知BC=8,OB=10![]() ,則另一直角邊AB的長(zhǎng)為__________.
,則另一直角邊AB的長(zhǎng)為__________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,ABCO的頂點(diǎn)A,B的坐標(biāo)分別是A(3,0),B(0,2),動(dòng)點(diǎn)P在直線y=![]() x上運(yùn)動(dòng),以點(diǎn)P為圓心,PB長(zhǎng)為半徑的⊙P隨點(diǎn)P運(yùn)動(dòng),當(dāng)⊙P與四邊形ABCO的邊所在直線相切時(shí),P點(diǎn)的坐標(biāo)為_____.
x上運(yùn)動(dòng),以點(diǎn)P為圓心,PB長(zhǎng)為半徑的⊙P隨點(diǎn)P運(yùn)動(dòng),當(dāng)⊙P與四邊形ABCO的邊所在直線相切時(shí),P點(diǎn)的坐標(biāo)為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)![]() 四點(diǎn)在一條直線上,
四點(diǎn)在一條直線上,![]() ,
,![]() .老師說(shuō):再添加一個(gè)條件就可以使
.老師說(shuō):再添加一個(gè)條件就可以使![]() .下面是課堂上三個(gè)同學(xué)的發(fā)言,甲說(shuō):添加
.下面是課堂上三個(gè)同學(xué)的發(fā)言,甲說(shuō):添加![]() ;乙說(shuō):添加
;乙說(shuō):添加![]() ;丙說(shuō):添加
;丙說(shuō):添加![]() .
.

(1)甲、乙、丙三個(gè)同學(xué)說(shuō)法正確的是________
(2)請(qǐng)你從正確的說(shuō)法中選擇一種,給出你的證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 的
的![]() 與
與![]() 的部分對(duì)應(yīng)值如下表:
的部分對(duì)應(yīng)值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
則下列判斷中正確的是( )
A. 拋物線開(kāi)口向上 B. 拋物線與![]() 軸交于負(fù)半軸
軸交于負(fù)半軸
C. 當(dāng)![]() 時(shí),
時(shí),![]() D. 方程
D. 方程![]() 的正根在3與4之間
的正根在3與4之間
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】問(wèn)題:如圖①,在直角三角形![]() 中,
中,![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,可知
,可知![]() (不需要證明);
(不需要證明);
(1)探究:如圖②,![]() ,射線
,射線![]() 在這個(gè)角的內(nèi)部,點(diǎn)
在這個(gè)角的內(nèi)部,點(diǎn)![]() 、
、![]() 在
在![]() 的邊
的邊![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() .證明:
.證明:![]() ;
;
(2)證明:如圖③,點(diǎn)![]() 、
、![]() 在
在![]() 的邊
的邊![]() 、
、![]() 上,點(diǎn)
上,點(diǎn)![]() 、
、![]() 在
在![]() 內(nèi)部的射線
內(nèi)部的射線![]() 上,
上,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的外角。已知
的外角。已知![]() ,
,![]() .求證:
.求證:![]() ;
;
(3)應(yīng)用:如圖④,在![]() 中,
中,![]() ,
,![]() .點(diǎn)
.點(diǎn)![]() 在邊
在邊![]() 上,
上,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 在線段
在線段![]() 上,
上,![]() .若
.若![]() 的面積為15,則
的面積為15,則![]() 與
與![]() 的面積之和為_(kāi)_______.
的面積之和為_(kāi)_______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,對(duì)稱軸為
,對(duì)稱軸為![]() .
.
![]() 試用含
試用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 、
、![]() .
.
![]() 當(dāng)拋物線與直線
當(dāng)拋物線與直線![]() 交于點(diǎn)
交于點(diǎn)![]() 時(shí),求此拋物線的解析式.
時(shí),求此拋物線的解析式.
![]() 求當(dāng)
求當(dāng)![]() 取得最大值時(shí)的拋物線的頂點(diǎn)坐標(biāo).
取得最大值時(shí)的拋物線的頂點(diǎn)坐標(biāo).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com