
 如圖,CD是Rt△ABC斜邊上的高,∠ACB=90°,BC=2,AB=3.
如圖,CD是Rt△ABC斜邊上的高,∠ACB=90°,BC=2,AB=3.分析 (1)證明△ACD∽△CBD,然后根據相似三角形的對應邊的比相等即可證得;
(2)根據相似三角形的性質即可得到結論.
解答 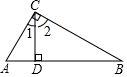 證明:∵Rt△ABC中,∠ACB=90°,
證明:∵Rt△ABC中,∠ACB=90°,
∴∠1+∠2=90°,
又∵CD是斜邊AB上的高
∴∠ADC=∠CDB=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•BD;
(2)∵∠ACB=90°,BC=2,AB=3,
∴AC=$\sqrt{5}$,
∴△ACD與△CBD的周長比=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$,△ACD與△CBD的面積比=($\frac{AC}{BC}$)2=$\frac{5}{4}$.
故答案為:$\frac{\sqrt{5}}{2}$,$\frac{5}{4}$.
點評 本題考查了相似三角形的判定與性質,證明等積式成立,常用的思路就是轉化為證明比例式,從而轉化為證明三角形相似.


 學業測評一課一測系列答案
學業測評一課一測系列答案 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案科目:初中數學 來源: 題型:選擇題
| A. | 圖象的開口向下 | B. | 當x>1時,y隨x的增大而減小 | ||
| C. | 當x<1時,y隨x的增大而減小 | D. | 圖象的對稱軸是直線x=-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$h | B. | 10h | C. | $\frac{80}{13}$ | D. | 以上答案都不對 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
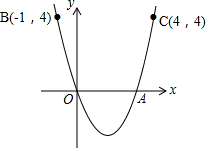 如圖,拋物線y=ax2+bx經過原點O,與x軸的另一個交點是A點,點B(-1,4)和點C(4,4)是拋物線上的兩個點,則點A的坐標為(3,0).
如圖,拋物線y=ax2+bx經過原點O,與x軸的另一個交點是A點,點B(-1,4)和點C(4,4)是拋物線上的兩個點,則點A的坐標為(3,0).查看答案和解析>>
科目:初中數學 來源:2016-2017學年四川省眉山市第九年級下學期第一次月考數學試卷(解析版) 題型:單選題
反比例函數 的圖象,當
的圖象,當 時,
時, 隨
隨 的增大而減小,則
的增大而減小,則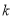 的取值范圍是( )
的取值范圍是( )
A.  B.
B.  C.
C. 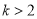 D.
D. 
查看答案和解析>>
科目:初中數學 來源:2016-2017學年江蘇省七年級下學期第一次月考數學試卷(解析版) 題型:判斷題
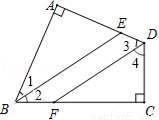
如圖,四邊形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,則BE與DF有何位置關系?試說明理由.
查看答案和解析>>
科目:初中數學 來源:2016-2017學年江蘇省七年級下學期第一次月考數學試卷(解析版) 題型:單選題
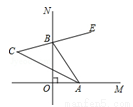
如圖,∠MON=90°,點A,B分別在射線OM,ON上運動,BE平分∠NBA, BE的反向延長線與∠BAO的平分線交于點C,則∠C的度數是( )
A. 30° B. 45° C. 55° D. 60°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com