
 如圖,在△ABC中,AB=6cm,BC=12cm,動點P從A開始沿AB邊運動,速度為2cm/s;動點Q從點B開始沿BC邊運動,速度為4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三點連成的三角形與△ABC相似.
如圖,在△ABC中,AB=6cm,BC=12cm,動點P從A開始沿AB邊運動,速度為2cm/s;動點Q從點B開始沿BC邊運動,速度為4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三點連成的三角形與△ABC相似. 分析 先用t表示出AP=2t,BQ=4t,BP=6-2t,再利用兩組對應邊的比相等且夾角對應相等的兩個三角形相似得到當$\frac{BP}{BA}$=$\frac{BQ}{BC}$時,△BPC∽△BAC或當$\frac{BP}{BC}$=$\frac{BQ}{BA}$時,△BPC∽△BCA,然后利用比例線段得到關于t的方程,再解方程求出t即可.
解答 解:如圖,AP=2t,BQ=4t,BP=6-2t,
∵∠PBC=∠ABC,
∴當$\frac{BP}{BA}$=$\frac{BQ}{BC}$時,△BPC∽△BAC,即$\frac{6-2t}{6}$=$\frac{4t}{12}$,解得t=$\frac{3}{2}$,
當$\frac{BP}{BC}$=$\frac{BQ}{BA}$時,△BPC∽△BCA,即$\frac{6-2t}{12}$=$\frac{4t}{6}$,解得t=$\frac{3}{5}$,
即當t=$\frac{3}{2}$s或$\frac{3}{5}$s時,由P、B、Q三點連成的三角形與△ABC相似.
故答案為$\frac{3}{2}$s或$\frac{3}{5}$.
點評 本題考查了相似三角形的判定:兩組對應邊的比相等且夾角對應相等的兩個三角形相似.注意分類討論思想的應用.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
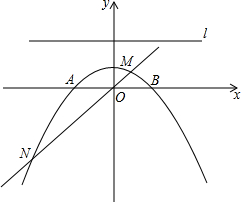 問題探究:
問題探究:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{x}{15}$-$\frac{10}{60}$=$\frac{x}{12}$+$\frac{2}{60}$ | B. | $\frac{x}{15}$+$\frac{10}{60}$=$\frac{x}{12}$-$\frac{2}{60}$ | ||
| C. | $\frac{x}{15}$+10=$\frac{x}{12}$-2 | D. | $\frac{x}{15}$-10=$\frac{x}{12}$+2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com