【題目】如圖，用同樣規格的黑白兩種正方形瓷磚鋪設正方形地面，觀察圖形并猜想填空：當黑色瓷磚為28塊時，白色瓷磚塊數為（ ）
A. 27 B. 28 C. 33 D. 35
【答案】D
【解析】分析：觀察題中，三個圖形的黑色瓷磚和白塊瓷磚所拼的圖形中，黑色瓷磚和白色瓷磚的個數的規律，列方程求解即可．
詳解：根據題目給出的圖，我們可以看出：
1圖中有黑色瓷磚12塊，我們把12可以改寫為3×4；白瓷磚的塊數為（1+1）2-1
2圖中有黑色瓷磚16塊，我們把16可以改寫為4×4；白瓷磚的塊數為（2+1）2-1
1圖中有黑色瓷磚20塊，我們把20可以改寫為5×4；白瓷磚的塊數為（3+1）2-1
……
第n個圖有（n+2）×4，也就是，有4n+8塊黑色的瓷磚；白瓷磚的塊數為（n+1）2-1．
所以4n+8=28
解得n=5
所以白瓷磚的塊數為（5+1）2-1=35.
故答案為：35.
學業測評一課一測系列答案科目：初中數學 來源： 題型：
【題目】如圖，一只甲蟲在5×5的方格(每小格邊長為1)上沿著網格線運動，它從A處出發看望B、C、D處的其它甲蟲．規定：向上向右走為正，向下向左走為負，如果從A到B記為：A→B(＋1，＋4)，從B到A記為：B→A(－1，－4)．其中第一數表示左右方向，第二個數表示上下方向，那么圖中
(1)A→C( ， )，B→D( ， )；
(2)若這只甲蟲的行走路線為A→B→C→D，請計算該甲蟲走過的路程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知正方形ABCD，P為射線AB上的一點，以BP為邊作正方形BPEF，使點F在線段CB的延長線上，連接EA、EC．
（1）如圖1，若點P在線段AB的延長線上，求證：EA=EC；
（2）若點P在線段AB上．如圖2，連接AC，當P為AB的中點時，判斷△ACE的形狀，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面的材料
勾股定理神秘而美妙，它的證法多種多樣，下面是教材中介紹的一種拼圖證明勾股定理的方法.
先做四個全等的直角三角形，設它們的兩條直角邊分別為a,b，斜邊為c，然后按圖1的方法將它們擺成正方形.
由圖1可以得到
，
整理，得
．
所以
．
如果把圖1中的四個全等的直角三角形擺成圖2所示的正方形，
請你參照上述證明勾股定理的方法，完成下面的填空：
由圖2可以得到 ，
整理，得 ，
所以 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】嘉淇準備完成題目：化簡：
，發現系數“
”印刷不清楚．
（1）他把“”猜成3，請你化簡：（3x2+6x+8）–（6x+5x2+2）；
（2）他媽媽說：“你猜錯了，我看到該題標準答案的結果是常數．”通過計算說明原題中“”是幾？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】給出如下結論：①單項式﹣
的系數為﹣
，次數為2；②當x=5，y=4時，代數式x2﹣y2的值為1；③化簡（x+
）﹣2（x﹣）的結果是﹣x+
；④若單項式
ax2yn+1與﹣
axmy4的和仍是單項式，則m+n=5．其中正確的結論是_____（填序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一次函數y=kx+b的圖像分別交x軸、y軸于A、B兩點．與反比例函數y=﹣ 
的圖像交于C，D兩點，DE⊥x軸于點E．已知DE=3，AE=6．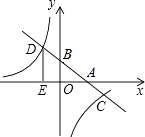 
（1）求一次函數的解析式；
（2）直接寫出不等式kx+b+ ＞0的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖1是一個八角星形紙板，圖中有八個直角、八個相等的鈍角，每條邊都相等，如圖2將紙板沿虛線進行切割，無縫隙無重疊的拼成如圖3所示的大正方形，其面積為8+4 
，則圖3中線段AB的長為（ ）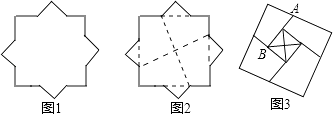 
A.
B.2
C. ﹣1
D. +1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
