
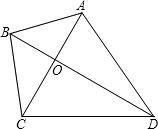
 已知四邊形ABCD兩條對角線互相垂直,點O是對角線的交點,∠ACD=60°,∠ABD=45°,點A到CD的距離是6,點D到AB的距離是8,求四邊形ABCD的面積S.
已知四邊形ABCD兩條對角線互相垂直,點O是對角線的交點,∠ACD=60°,∠ABD=45°,點A到CD的距離是6,點D到AB的距離是8,求四邊形ABCD的面積S.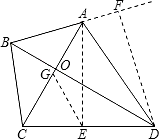 解:過點A作CD的垂線,E是垂足,過點D作AB的垂線,F是垂足,取AC的中點G,連接EG,
解:過點A作CD的垂線,E是垂足,過點D作AB的垂線,F是垂足,取AC的中點G,連接EG,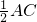 ,
,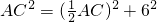 ,
, ,
,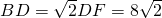 .
. BD•AO+
BD•AO+ BD•CO,
BD•CO,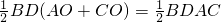 ,
,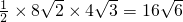 .
. .
.

 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
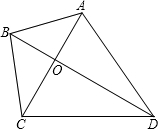 已知四邊形ABCD兩條對角線互相垂直,點O是對角線的交點,∠ACD=60°,∠ABD=45°,點A到CD的距離是6,點D到AB的距離是8,求四邊形ABCD的面積S.
已知四邊形ABCD兩條對角線互相垂直,點O是對角線的交點,∠ACD=60°,∠ABD=45°,點A到CD的距離是6,點D到AB的距離是8,求四邊形ABCD的面積S.查看答案和解析>>
科目:初中數學 來源: 題型:
 22、已知四邊形ABCD,請從下列條件中取兩個加以組合,得出四邊形ABCD是平行四邊形.(選4種組合,不需要證明.)
22、已知四邊形ABCD,請從下列條件中取兩個加以組合,得出四邊形ABCD是平行四邊形.(選4種組合,不需要證明.)查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知四邊形ABCD,對角線AC,BD相交于點O.僅從下列六項條件中任意選取兩項作為已知條件,就能夠確定四邊形ABCD是平行四邊形的方法有( )種
如圖,已知四邊形ABCD,對角線AC,BD相交于點O.僅從下列六項條件中任意選取兩項作為已知條件,就能夠確定四邊形ABCD是平行四邊形的方法有( )種查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com