
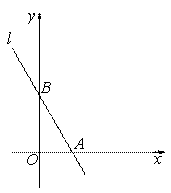
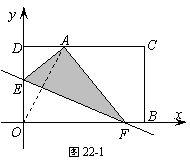
如圖,在平面直角坐標系中,點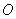 為坐標原點,直線
為坐標原點,直線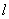 分別交
分別交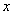 軸、
軸、 軸于
軸于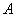 、
、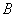 兩點,
兩點,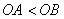 ,且
,且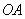 、
、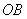 的長分別是一元二次方程
的長分別是一元二次方程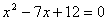 的兩根.
的兩根.
(1)求直線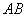 的函數表達式;
的函數表達式;
(2)點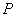 是
是 軸上的點,點
軸上的點,點 是第一象限內的點.若以
是第一象限內的點.若以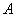 、
、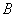 、
、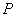 、
、
為頂點的四邊形是菱形,請直接寫出 點的坐標.
點的坐標.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
已知關于 的一元二次方程
的一元二次方程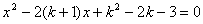 有兩個不相等的實數
有兩個不相等的實數 根.
根.
(1)求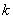 的取值范圍;
的取值范圍;
(2)當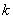 取最小的整數時,求拋物線
取最小的整數時,求拋物線 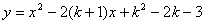 的頂點坐標以及它與
的頂點坐標以及它與 軸的交點坐標;
軸的交點坐標;
(3)將(2)中求得的拋物線在 軸下方的部分沿
軸下方的部分沿 軸翻折到
軸翻折到 軸上方,圖象的其余部分不變,得到一個新圖象.請你畫出這個新圖象,并求出新圖象與直線
軸上方,圖象的其余部分不變,得到一個新圖象.請你畫出這個新圖象,并求出新圖象與直線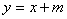 有三個不同公共點時
有三個不同公共點時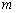 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
閱讀下列材料:
問題:在平面直角坐標系 中,一張矩形紙片
中,一張矩形紙片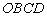 按圖1所示放置。已知
按圖1所示放置。已知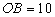 ,
,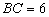 ,
,
將這張紙片折疊,使點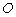 落在邊
落在邊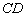 上,記作點
上,記作點 ,折痕與邊
,折痕與邊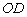 (含端點)交于點
(含端點)交于點 ,與邊
,與邊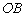 (含端
(含端
點)或其延長線交于點 ,求點
,求點 的坐標。
的坐標。
小明在解決這個問題時發現:要求點 的坐標,只要求出線段
的坐標,只要求出線段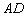 的長即可,連接
的長即可,連接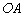 ,設折痕
,設折痕 所
所
在直線對應的函數表達式為: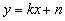
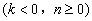 ,于是有
,于是有 ,
,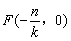 ,所以在
,所以在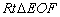
 中,得到
中,得到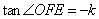 ,在
,在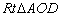 中,利用等角的三角函數值相等,就可以求出線段
中,利用等角的三角函數值相等,就可以求出線段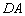 的長(如圖
的長(如圖
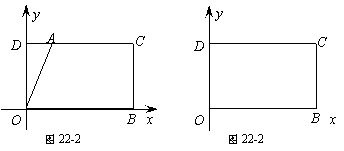 1)
1)
 |
請回答:
(1)如圖1,若點 的坐標為
的坐標為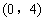 ,直接寫出點
,直接寫出點 的坐標;
的坐標;
(2)在圖2中,已知點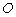 落在邊
落在邊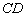 上的點
上的點 處,請畫出折痕所在的直線
處,請畫出折痕所在的直線 (要求:尺規作圖,保留作圖痕跡,不寫做法);
(要求:尺規作圖,保留作圖痕跡,不寫做法);
參考小明的做法,解決以下問題:
(3)將矩形沿直線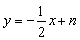 折疊,求點
折疊,求點 的坐標;
的坐標;
(4)將矩形沿直線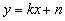 折疊,點
折疊,點 在邊
在邊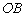 上(含端點),直接寫出
上(含端點),直接寫出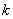 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com