
【題目】如圖,直線 ![]() 1:y=kx+b 分別交 x 軸、y 軸于點 B(4,0)、N,直線
1:y=kx+b 分別交 x 軸、y 軸于點 B(4,0)、N,直線![]() 2:y=2x-1分別交 x 軸、y 軸于點 M、A,
2:y=2x-1分別交 x 軸、y 軸于點 M、A,![]() 1,
1,![]() 2 交點 P 的坐標(m,2),請根據圖象所提供的信息解答下列問題:
2 交點 P 的坐標(m,2),請根據圖象所提供的信息解答下列問題:

(1)當 x 時,kx+b≥2x-1;
(2)不等式 k![]() +b<0 的解集是 ;
+b<0 的解集是 ;
(3)在平面內是否存在一點 H,使得以A,B,P,H四點組成的四邊形是平行四邊形.若存在,直接寫出點 H 的坐標,若不存在,說明理由.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)存在,點H的坐標為(
; (3)存在,點H的坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求得點P的坐標,根據函數圖象,即可求解;
(2)根據函數圖象,即可求解;
(3)設點H的坐標為(a,n),分AB為對角線、AP為對角線及BP為對角線三種情況,利用平行四邊形的性質(對角線互相平分)可求出點H的坐標.
(1)∵點P(m,2)在直線![]() 2:
2:![]() 上,
上,
令![]() ,則
,則![]() ,
,
∴點P的坐標為(![]() ,2),
,2),
觀察函數圖象,當![]() 時,直線
時,直線 ![]() 1在直線
1在直線![]() 2的上方,
2的上方,
∴當![]() 時,
時,![]() ;
;
(2)直線 ![]() 1:
1:![]() 分別交
分別交![]() 軸于點 B(4,0),
軸于點 B(4,0),
觀察函數圖象,當![]() 時,直線
時,直線 ![]() 1在
1在![]() 軸的下方,
軸的下方,
∴不等式![]() 的解集為:
的解集為:![]() ;
;
(3)存在,設點H的坐標為(a,n),
令![]() ,則
,則![]() ,
,
∴點A的坐標為(0,![]() ),
),
∵點B的坐標為(4,0),點P的坐標為(![]() ,2),
,2),
分三種情況考慮,如圖所示:
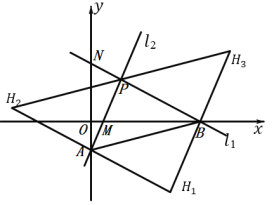
①當AB為對角線時,
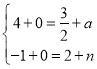
解得: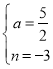 ,
,
∴點![]() 的坐標為(
的坐標為(![]() ,
,![]() );
);
②當AP為對角線時,
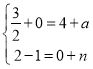 ,
,
解得: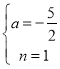 ,
,
∴點![]() 的坐標為(
的坐標為(![]() ,
,![]() );
);
③當BP為對角線時,
 ,
,
解得: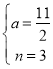 ,
,
∴點![]() 的坐標為(
的坐標為(![]() ,
,![]() );
);
綜上所述:在平面直角坐標系中存在點H,使以點A,B,P,H為頂點的四邊形是平行四邊形,點H的坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .


科目:初中數學 來源: 題型:
【題目】某蔬菜有限公司一年四季都有大量新鮮蔬菜銷往全國各地,近年來它的蔬菜產值不斷增加,2014年蔬菜的產值是640萬元,2016年產值達到1000萬元.
(1)求2015年、2016年蔬菜產值的平均增長率是多少?
(2)若2017年蔬菜產值繼續穩定增長(即年增長率與前兩年的年增長率相同),那么請你估計2017年該公司的蔬菜產值達到多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將平行四邊形 ABCD 沿對角線 BD 折疊,使點 A 落在A′處,若∠1=∠2=50°,則∠A′的度數為( )

A.100°B.105°C.110°D.115°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點G,D,C在直線a上,點E,F,A,B在直線b上,若a∥b,Rt△GEF從如圖所示的位置出發,沿直線b向右勻速運動,直到EG與BC重合.運動過程中△GEF與矩形ABCD重合部分的面積(S)隨時間(t)變化的圖象大致是( )

A.  B.
B.  C.
C. 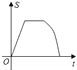 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
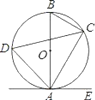
【題目】如圖,已知AB是⊙O的直徑,點C、D在⊙O上,點E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度數;
(2)求證:AE是⊙O的切線;
(3)當BC=4時,求劣弧AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,如圖1,將線段AB平移至線段CD,連接AC、BD.

(1)已知A(﹣3,0)、B(﹣2,﹣2),點C在y軸的正半軸上,點D在第一象限內,且三角形ACO的面積是6,求點C、D的坐標;
(2)如圖2,在平面直角坐標系中,已知一定點M(1,0),兩個動點E(a,2a+1)、F(b,﹣2b+3).
①請你探索是否存在以兩個動點E、F為端點的線段EF平行于線段OM且等于線段OM,若存在,求出點E、F兩點的坐標;若不存在,請說明理由;
②當點E、F重合時,將該重合點記為點P,另當過點E、F的直線平行于x軸時,是否存在△PEF的面積為2?若存在,求出點E、F兩點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測量學校教學樓的高度,王芳同學在她的腳下放了一面鏡子,然后向后退,直到她剛好在鏡子中看到樓的頂部.如果王芳同學的身高是1.55m,她估計自己的眼睛距地面AB=1.50m,同時量得BE=30cm,BD=2.3m,這棟樓CD有多高?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com