

分析 (1)設動點A的速度是t單位長度/秒,那么動點B的速度是3t單位長度/秒,然后根據4秒后,兩點相距16個單位長度即可列出方程解決問題;
(2)設y秒時,原點恰好處在兩個動點的正中間,那么A運動的長度為y,B運動的長度為3y,然后根據(1)的結果和已知條件即可列出方程解題;
(3)設當C運動z秒后,C為AB的中點,由中點坐標公式就可以求出結論.
解答 解:(1)設點A的速度為每秒t個單位長度,則點B的速度為每秒3t個單位長度.
依題意有:4t+4×3t=16,
解得:t=1,
故點A的速度為每秒1個單位長度,點B的速度為每秒3個單位長度,
則A到達的位置為:-4,B到達的位置是12,在數軸上的位置如圖: ,
,
答:點A的速度為每秒1個單位長度,點B的速度為每秒3個單位長度;
(2)設y秒時,原點恰好處在兩個動點的正中間,根據題意得:
4+y=12-3y
解得:y=2,
答:2秒時,原點恰好處在AB的中點;
(3)設當C運動z秒后,C為AB的中點,
由題意可得:4+z+$\frac{1}{2}$z=$\frac{1}{2}$(16-3z+z),
解得:z=$\frac{8}{5}$,
答:當點C運動$\frac{8}{5}$秒時,C為AB的中點.
點評 此題主要考查了一元一次方程的應用,關鍵是正確理解題意,找出題目中的等量關系,設出未知數,列出方程.


 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:初中數學 來源: 題型:解答題
 如圖,正方形ABCD的邊長為6,E,F分別是AB,BC邊上的點,且∠EDF=45°,將△DAE繞點D逆時針旋轉90°,得到△DCM.
如圖,正方形ABCD的邊長為6,E,F分別是AB,BC邊上的點,且∠EDF=45°,將△DAE繞點D逆時針旋轉90°,得到△DCM.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
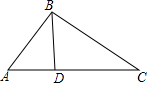 如圖,在△ABC中,D是AC上一點,聯結BD,∠CBD=∠A.
如圖,在△ABC中,D是AC上一點,聯結BD,∠CBD=∠A.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com