
【題目】解方程
(1) 3x-2(x-1)= 2- 3(5-2x)
(2)![]()
(3)![]()
(4) ![]()
【答案】(1)x=3;(2)x=5;(3)x=-8;(4)x=-9.2
【解析】
(1)去括號,移項,合并同類項,系數化為1可得;(2)去分母,去括號,移項,合并同類項,系數化為1可得;(3)去括號,移項,合并同類項,系數化為1可得;(4)去分母,去括號,移項,合并同類項,系數化為1可得;
解:(1) 3x-2(x-1)= 2- 3(5-2x)
3x-2x+2=2-15+6x
3x-2x-6x=2-15-2
-5x=-15
x=3
(2)![]()
4(x+1)=5(x+1)-6
4x+4=5x+5-6
4x-5x=5-6-4
-x=-5
x=5
(3)![]()
![]()
![]()
![]()
![]()
x=-8
(4) ![]()
2(x-3)-5(x+4)=1.6
2x-6-5x-20=1.6
2x-5x=1.6+6+20
-3x=27.6
x=-9.2


科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C是⊙O上一點,過點C的直線交AB的延長線于點D,AE⊥DC,垂足為E,F是AE與⊙O的交點,AC平分∠BAE.

(1)求證:DE是⊙O的切線;
(2)若AE=6,∠D=30°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了改善辦公條件,計劃從廠家購買A、B兩種型號電腦。已知每臺A種型號電腦價格比每臺B種型號電腦價格多0.1萬元,且用10萬元購買A種型號電腦的數量與用8萬元購買B種型號電腦的數量相同.
(1)求A、B兩種型號電腦每臺價格各為多少萬元?
(2)學校預計用不多于9.2萬元的資金購進這兩種電腦共20臺,則最多可購買A種型號電腦多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍,設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
①求y關于x的函數關系式;
②該商店購進A型、B型電腦各多少臺,才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺,若商店保持同種電腦的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺電腦銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB=AC,AD為∠BAC的角平分線,D、E、F…為∠BAC的角平分線上的若干點.如圖1,連接BD、CD,圖中有1對全等三角形;如圖2,連接BD、CD、BE、CE,圖中有3對全等三角形;如圖3,連接BD、CD、BE、CE、BF、CF,圖中有6對全等三角形;依此規律,第n個圖形中有_____對全等三角形.
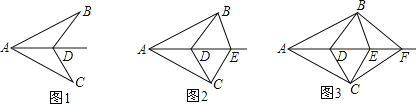
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 是
是![]() 邊上的一個動點,連接
邊上的一個動點,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() ,頂點
,頂點![]() 在線段
在線段![]() 上,對角線
上,對角線![]() 、
、![]() 相交于點
相交于點![]() .(1)若
.(1)若![]() ,則
,則![]() ;
;
(2)①求證:點![]() 一定在
一定在![]() 的外接圓上;
的外接圓上;
②當點![]() 從點
從點![]() 運動到點
運動到點![]() 時,點
時,點![]() 也隨之運動,求點
也隨之運動,求點![]() 經過的路徑長;
經過的路徑長;
(3)在點![]() 從點
從點![]() 到點
到點![]() 的運動過程中,
的運動過程中,![]() 的外接圓的圓心也隨之運動,求該圓心到
的外接圓的圓心也隨之運動,求該圓心到![]() 邊的距離的最大值.
邊的距離的最大值.
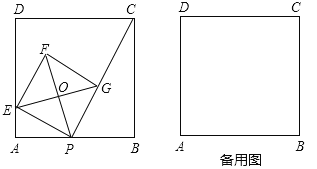
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC,(1)如圖①,若P點是∠ABC和∠ACB的角平分線的交點,則∠P=90°+![]() ∠A;(2)如圖②,若P點是∠ABC和外角∠ACE的角平分線的交點,則∠P=90°-∠A;(3)如圖③,若P點是外角∠CBF和∠BCE的角平分線的交點,則∠P=90°-
∠A;(2)如圖②,若P點是∠ABC和外角∠ACE的角平分線的交點,則∠P=90°-∠A;(3)如圖③,若P點是外角∠CBF和∠BCE的角平分線的交點,則∠P=90°-![]() ∠A.上述說法正確的個數是( )
∠A.上述說法正確的個數是( )

A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小巷左右兩側是豎直的墻,一架梯子![]() 斜靠在左墻時,梯子底端到左墻角的距離
斜靠在左墻時,梯子底端到左墻角的距離![]() 為0.7米,頂端到地面距離
為0.7米,頂端到地面距離![]() 為2.4米,如果保持梯子底端位置不動,將梯子斜靠在右墻時,頂端到地面距離
為2.4米,如果保持梯子底端位置不動,將梯子斜靠在右墻時,頂端到地面距離![]() 為2米,求小巷的寬度
為2米,求小巷的寬度![]() .
.
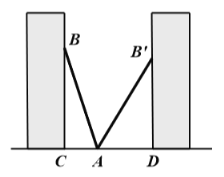
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校要從小王和小李兩名同學中挑選一人參加全市知識競賽,在最近的五次選拔測試中,他倆的成績分別如下表:
姓 名 | 1 | 2 | 3 | 4 | 5 |
小 王 | 60 | 75 | 100 | 90 | 75 |
小 李 | 70 | 90 | 80 | 80 | 80 |
根據上表解答下列問題:
(1)完成下表:
姓 名 | 平均成績(分) | 中位數(分) | 眾數(分) | 方差 |
小 王 | 75 | 190 | ||
小 李 | 80 | 80 |
(2)在這五次測試中,成績比較穩定的同學是誰?若將80分以上(含80分)的成績視為秀,則小王、小李在這五次測試中的優秀率各是多少?
(3)歷屆比賽表明,成績達到80分以上(含80分)就很可能獲獎,成績達到90分以上(含90分)就很可能獲得一等獎,那么你認為選誰參加比賽比較合適?說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com