
【題目】閱讀理解:如果兩個正數a,b,即a>0,b>0,有下面的不等式:![]() ,當且僅當a=b時取到等號我們把
,當且僅當a=b時取到等號我們把![]() 叫做正數a,b的算術平均數,把
叫做正數a,b的算術平均數,把![]() 叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最值問題的有力工具.
叫做正數a,b的幾何平均數,于是上述不等式可表述為:兩個正數的算術平均數不小于(即大于或等于)它們的幾何平均數.它在數學中有廣泛的應用,是解決最值問題的有力工具.
初步探究:(1)已知x>0,求函數y=x+![]() 的最小值.
的最小值.
問題遷移:(2)學校準備以圍墻一面為斜邊,用柵欄圍成一個面積為100m2的直角三角形,作為英語角,直角三角形的兩直角邊各為多少時,所用柵欄最短?
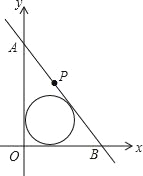
創新應用:(3)如圖,在直角坐標系中,直線AB經點P(3,4),與坐標軸正半軸相交于A,B兩點,當△AOB的面積最小時,求△AOB的內切圓的半徑.
【答案】初步探究:(1)4;問題遷移:(2)x=10![]() m時,y有最小值,即所用柵欄最短;創新應用:(3)R=2.
m時,y有最小值,即所用柵欄最短;創新應用:(3)R=2.
【解析】
(1)根據x>0,令a=x,b=![]() ,利用題中的新定義求出函數的最小值即可;
,利用題中的新定義求出函數的最小值即可;
(2)設一直角邊為xm,則另一直角邊為![]() m,柵欄總長為ym,根據題意表示出y與x的函數關系式,利用題中的新定義求出y取得最小值時x的值即可;
m,柵欄總長為ym,根據題意表示出y與x的函數關系式,利用題中的新定義求出y取得最小值時x的值即可;
(3)設直線AB解析式為y=kx+b,把P坐標代入用k表示出b,進而表示出A與B坐標,確定出OA與OB的長,得出三角形AOB面積,利用題中的新定義求出三角形AOB面積最小時k的值,確定出直角三角形三邊,即可求出三角形AOB內切圓半徑.
解:(1)令a=x,b=![]() (x>0),
(x>0),
由a+b≥2![]() ,得y=x+
,得y=x+![]() ≥2
≥2![]() =4,
=4,
當且僅當x=![]() 時,即x=2時,函數有最小值,最小值為4;
時,即x=2時,函數有最小值,最小值為4;
(2)設一直角邊為xm,則另一直角邊為![]() m,柵欄總長為ym,
m,柵欄總長為ym,
y=x+![]() ,
,
當且僅當x=![]() 時,即x=10
時,即x=10![]() m時,y有最小值,即所用柵欄最短;
m時,y有最小值,即所用柵欄最短;
(3)設直線AB的解析式是y=kx+b,
把P(3,4)代入得:4=3k+b,
整理得:b=4﹣3k,
∴直線AB的解析式是y=kx+4﹣3k,
當x=0時,y=4﹣3k;當y=0時,x=![]() ,
,
即A(0,4﹣3k),B(![]() ,0),
,0),
∴S△AOB=![]() OBOA=
OBOA=![]() (4﹣3k)
(4﹣3k)![]() =12﹣(
=12﹣(![]() ),
),
∵要使△AOB的面積最小,
∴![]() 必須最大,
必須最大,
∵k<0,
∴﹣k>0,
∵![]() =2×6=12,當且僅當
=2×6=12,當且僅當![]() 時,取等號,
時,取等號,
解得:k=±![]() ,
,
∵k<0,
∴k=﹣![]() ,
,
即OA=4﹣3k=8,OB=6,
根據勾股定理得:AB=10,
設三角形AOB的內切圓的半徑是R,
由三角形面積公式得:![]() ×6×8=
×6×8=![]() ×6R+
×6R+![]() ×8R+
×8R+![]() ×10R,
×10R,
解得:R=2.


科目:初中數學 來源: 題型:
【題目】某校八年級舉行英語演講比賽,準備用1200元錢(全部用完)購買A,B兩種筆記本作為獎品,已知A,B兩種每本分別為12元和20元,設購入A種x本,B種y本.
(1)求y關于x的函數表達式.
(2)若購進A種的數量不少于B種的數量.
①求至少購進A種多少本?
②根據①的購買,發現B種太多,在費用不變的情況下把一部分B種調換成另一種C,調換后C種的數量多于B種的數量,已知C種每本8元,則調換后C種至少有______本(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線![]() ,經過點A(-1,-2),B(0,1).
,經過點A(-1,-2),B(0,1).
(1)求拋物線的關系式及頂點P的坐標.
(2)若點B′與點B關于x軸對稱,把(1)中的拋物線向左平移m個單位,平移后的拋物線經過點B′,設此時拋物線頂點為點P′.
①求∠P′B B′的大小.
②把線段P′B′以點B′為旋轉中心順時針旋轉120°,點P′落在點M處,設點N在(1)中的拋物線上,當△MN B′的面積等于6![]() 時,求點N的坐標.
時,求點N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是等腰直角△ABC外一點,把BP繞點B順時針旋轉90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,則P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,∠A=90°.
(1)請用圓規和直尺作出⊙P,使圓心P在AC邊上,且與AB,BC兩邊都相切(保留作圖痕跡,不寫作法和證明);

(2)在(1)的條件下,若∠B=45°,AB=1,⊙P切BC于點D,求劣弧![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
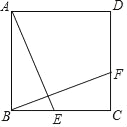
【題目】如圖,正方形ABCD中,點E、F分別在邊BC和DC上,連接AE、BF,AE⊥BF,點M、N分別在邊AB、DC上,連接MN,若MN∥BC,FN=1,BE=2,則BM=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() :
:![]() 與直線
與直線![]() :
:![]() 交于點
交于點![]() ,則
,則![]() ______.
______.

【答案】-1
【解析】
將點A的坐標代入兩直線解析式得出關于m和b的方程組,解之可得.
解:由題意知![]() ,
,
解得![]() ,
,
故答案為:![]() .
.
【點睛】
本題主要考查兩直線相交或平行問題,解題的關鍵是掌握兩直線的交點坐標必定同時滿足兩個直線解析式.
【題型】填空題
【結束】
11
【題目】如圖,長方形紙片ABCD中,AB=4,BC=6,將△ABC沿AC折疊,使點B落在點E處,CE交AD于點F,則△AFC的面積等于___.

查看答案和解析>>
科目:初中數學 來源: 題型:
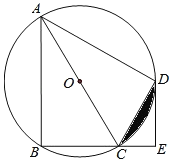
【題目】如圖,四邊形ABCD是⊙O的內接四邊形,AC為直徑,![]() ,DE⊥BC,垂足為E.
,DE⊥BC,垂足為E.
(1)判斷直線ED與⊙O的位置關系,并說明理由;
(2)若CE=1,AC=4,求陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com