Question

14．如圖，在邊長為6的正方形ABCD中，點E為AD邊上的一個動點（與點A、D不重合），∠EBM=45°，BE交對角線AC于點F，BM交對角線AC于點G，交CD于點M．
（1）如圖1，聯結BD，求證：△DEB∽△CGB，并寫出DE：CG的值；
（2）聯結EG，如圖2，若設AE=x，EG=y，求y關于x的函數解析式，并寫出函數的定義域；
（3）當M為邊DC的三等分點時，求S_△EGF的面積．

Answer 1

分析 （1）根據正方形的性質得到∠EDB=∠GCB=45°，∠ABD=∠CBD=45°，根據相似三角形的判定定理證明即可；
（2）作EH⊥AC于H，根據等腰直角三角形的性質、勾股定理和相似三角形的性質得到y關于x的函數解析式；
（3）分CM=$\frac{1}{3}$CD和CM=$\frac{2}{3}$CD兩種情況，根據相似三角形的性質解答即可．

解答 （1）證明：∵四邊形ABCD是正方形，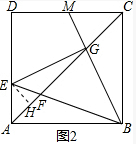
∴∠EDB=∠GCB=45°，∠ABD=∠CBD=45°，又∠EBM=45°，
∴∠GBC+∠DBM=45°，∠EBD+∠DBM=45°，
∴∠GBC=∠EBD，又∠EDB=∠GCB=45°，
∴△DEB∽△CGB，
∴DE：CG=BD：BC=$\sqrt{2}$；
（2）如圖2，作EH⊥AC于H，
則AH=EH=$\frac{\sqrt{2}}{2}$x，
∵△DEB∽△CGB，
∴$\frac{CG}{DE}$=$\frac{BC}{BD}$=$\frac{\sqrt{2}}{2}$，
∴CG=$\frac{\sqrt{2}}{2}$（6-x），
∴HG=AC-AH-CG=3$\sqrt{2}$，
∵EG²=EH²+HG²，
∴y=$\frac{\sqrt{2{x}^{2}+72}}{2}$（0＜x＜6）；
（3）當CM=$\frac{1}{3}$CD=2時，
∵四邊形ABCD是正方形，
∴CD∥AB，
∴$\frac{CM}{AB}$=$\frac{CG}{AG}$=$\frac{1}{3}$，
∴CG=$\frac{3}{2}\sqrt{2}$，
∴DE=3，則AE=3，
∴AH=EH=$\frac{3}{2}\sqrt{2}$，
∵AD∥BC，
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$=$\frac{1}{2}$，
∴AF=2$\sqrt{2}$，
∴GF=AC-AF-CG=$\frac{5}{2}$$\sqrt{2}$，
∴S_△EGF=$\frac{1}{2}$×FG×EH=$\frac{15}{4}$，
當CM=$\frac{2}{3}$CD=4時，
$\frac{CM}{AB}$=$\frac{CG}{AG}$=$\frac{2}{3}$，
∴CG=$\frac{12}{5}$$\sqrt{2}$，
∴DE=$\frac{24}{5}$，則AE=$\frac{6}{5}$，
AH=EH=$\frac{3\sqrt{2}}{5}$，
∵$\frac{AE}{BC}=\frac{AF}{CF}=\frac{1}{5}$，
∴AF=$\sqrt{2}$，
∴GF=AC-AF-CG=$\frac{13\sqrt{2}}{5}$，
∴S_△EGF=$\frac{1}{2}$×FG×EH=$\frac{39}{25}$．

點評 本題考查的是相似三角形的判定和性質的應用、正方形的性質的應用，正確作出輔助線、靈活運用相關的定理是解題的關鍵，注意分情況討論思想的運用．