
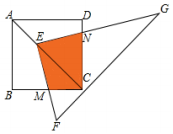
 如圖,點E在正方形ABCD的對角線AC上,且EC=2AE,直角三角形FEG的兩直角邊EF,EG分別交BC,DC于點M,N,若正方形ABCD的邊長為a,則重疊部分四邊形EMCN的面積為$\frac{4}{9}$a2.
如圖,點E在正方形ABCD的對角線AC上,且EC=2AE,直角三角形FEG的兩直角邊EF,EG分別交BC,DC于點M,N,若正方形ABCD的邊長為a,則重疊部分四邊形EMCN的面積為$\frac{4}{9}$a2. 分析 過E作EP⊥BC于點P,EQ⊥CD于點Q,△EPM≌△EQN,利用四邊形EMCN的面積等于正方形PCQE的面積求解.
解答 解:過E作EP⊥BC于點P,EQ⊥CD于點Q,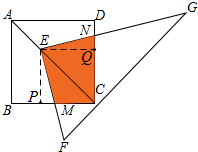
∵四邊形ABCD是正方形,
∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分線,∠EPC=∠EQC=90°,
∴EP=EQ,四邊形PCQE是正方形,
在△EPM和△EQN中,
$\left\{\begin{array}{l}{∠PEM=∠NEQ}\\{EP=EQ}\\{∠EPM=∠EQN}\end{array}\right.$,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四邊形EMCN的面積等于正方形PCQE的面積,
∵正方形ABCD的邊長為a,
∴AC=$\sqrt{2}$a,
∵EC=2AE,
∴EC=$\frac{2\sqrt{2}}{3}$a,
∴EP=PC=$\frac{2}{3}$a,
∴正方形PCQE的面積=$\frac{2}{3}$a×$\frac{2}{3}$a=$\frac{4}{9}$a2,
∴四邊形EMCN的面積=$\frac{4}{9}$a2,
故答案為:$\frac{4}{9}$a2.
點評 本題主要考查了正方形的性質及全等三角形的判定及性質,解題的關鍵是作出輔助線,證出△EPM≌△EQN.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:填空題
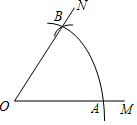 如圖,以O為圓心,任意長為半徑畫弧,與射線OM交于點A,再以A為圓心,AO為半徑畫弧,兩弧交于點B,畫射線OB,則sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.
如圖,以O為圓心,任意長為半徑畫弧,與射線OM交于點A,再以A為圓心,AO為半徑畫弧,兩弧交于點B,畫射線OB,則sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
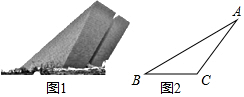 位于合肥濱湖新區的渡江戰役紀念館,實物圖如圖1所示,示意圖如圖2所示.某學校數學興趣小組通過測量得知,紀念館外輪廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求館頂A離地面BC的距離.(結果精確到0.1m,參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
位于合肥濱湖新區的渡江戰役紀念館,實物圖如圖1所示,示意圖如圖2所示.某學校數學興趣小組通過測量得知,紀念館外輪廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求館頂A離地面BC的距離.(結果精確到0.1m,參考數據:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
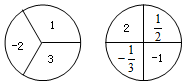 如圖,甲轉盤被分成 3 個面積相等的扇形,乙轉盤被分成 4 個面積相等的扇形,每一個扇形都標有相應的數字.同時轉動兩個轉盤,當轉盤停止后,設甲轉盤中指針所指區域內的數字為x,乙轉盤中指針所指區域內的數字為y(當指針指在邊界線上時,重轉,直到指針指向一個區域為止).
如圖,甲轉盤被分成 3 個面積相等的扇形,乙轉盤被分成 4 個面積相等的扇形,每一個扇形都標有相應的數字.同時轉動兩個轉盤,當轉盤停止后,設甲轉盤中指針所指區域內的數字為x,乙轉盤中指針所指區域內的數字為y(當指針指在邊界線上時,重轉,直到指針指向一個區域為止).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com