Question

如圖，△ABC內接于⊙O，高BE、AD交于點P．延長BD、CE，分別交⊙O于點M、N．求證：

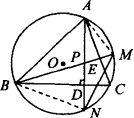
(1)PE＝ME，PD＝ND．

(2)點C為△PMN的外心．

Answer 1

答案：
解析：

解答：(1)連結AM、BN． 　　∵BD、CE是高， 　　∴∠CBE＋∠ACB＝∠CAD＋∠ACB＝90°，∴∠CBE＝∠CAD． 　　∵∠CBE＝∠CAM，∴∠CAD＝∠CAM． 　　∵AE＝AE，∠AEP＝∠AEM＝90°，∴△AEP≌△AEM(SAS)． 　　∴PE＝ME． 　　同法可證　　△BDP≌△BDN，故PD＝ND; 　　(2)由(1)知PE＝ME，AC⊥PM，∴AC垂直平分PM． 　　同理可得BC垂直平分PN． 　　∴點C為△PMN的兩邊PM、PN的垂直平分線的交點(易得：CM＝CP＝CN)，∴點C為△PMN的外心． 　　評析：這是關于三角形外接圓的又一研究，其中的諸多等線段的證明在近年來的不少中考試題中都曾有所出現．

提示：

欲證PE＝ME，PD＝ND，即需證AC垂直平分PM，BC垂直平分PN．