
【題目】某商店需要購進A.B兩種商品共160件,其進價和售價如表:
A | B | |
進價(元/件) | 15 | 35 |
售價(元/件) | 20 | 45 |
(1)當A.B兩種商品分別購進多少件時,商店計劃售完這批商品后能獲利1100元;
(2)若商店計劃購進A種商品不少于66件,且銷售完這批商品后獲利多于1260元,請你幫該商店老板預算有幾種購貨方案?獲利最大是多少元?
【答案】(1)甲種商品購進100件,乙種商品購進60件.(2)方案一:甲種商品購進66件,乙種商品購進94件.方案二:甲種商品購進67件,乙種商品購進93件,其中獲利最大的是方案一.
【解析】
(1)等量關系為:甲件數+乙件數=160;甲總利潤+乙總利潤=1100.
(2)設出所需未知數,甲數量+乙數量≥66;甲總利潤+乙總利潤>1260.
解:(1)設甲種商品應購進x件,乙種商品應購進y件.
根據題意得:![]() .解得:
.解得:![]() .
.
答:甲種商品購進100件,乙種商品購進60件.
(2)設甲種商品購進a件,則乙種商品購進(160﹣a)件.
根據題意得![]() .解不等式組,得66≤a<68.
.解不等式組,得66≤a<68.
∵a為非負整數,∴a取66,67.∴160﹣a相應取94,93.
方案一:甲種商品購進66件,乙種商品購進94件.
方案二:甲種商品購進67件,乙種商品購進93件.
最大獲利為;66×5+94×10=1270元;答:有兩種購貨方案,其中獲利最大的是方案一.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:
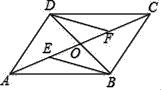
【題目】如圖所示,四邊形ABCD的對角線AC、BD交于點O,若OE=OF,DF∥BE.
(1)求證:△BOE≌△DOF;
(2)求證:四邊形DEBF是平行四邊形;
(3)若OD=OE=OF,則四邊形DEBF是什么特殊的四邊形,請證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了滿足學生借閱圖書的需求,計劃購買一批新書.為此,該校圖書管理員對一周內本校學生從圖書館借出各類圖書的數量進行了統計,結果如下圖.

請你根據統計圖中的信息,解答下列問題:
(1)補全條形圖和扇形圖;
(2)該校學生最喜歡借閱哪類圖書?
(3)該校計劃購買新書共600本,若按扇形統計圖中的百分比來相應地確定漫畫、科普、文學、其它這四類圖書的購買量,求應購買這四類圖書各多少本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 已知反比例函數y=![]() 的圖象與一次函數y=ax+b的圖象交于M(2,m)和N(-1,-4)兩點.
的圖象與一次函數y=ax+b的圖象交于M(2,m)和N(-1,-4)兩點.
(1)求這兩個函數的解析式;
(2)求△MON的面積;
(3)請判斷點P(4,1)是否在這個反比例函數的圖象上,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在ABCD中,延長DA到點E,延長BC到點F,使得AE=CF,連接EF,分別交AB,CD于點M,N,連接DM,BN.
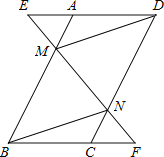
(1)求證:△AEM≌△CFN;
(2)求證:四邊形BMDN是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,對任意一個正整數n都可以進行這樣的分解:n=p![]() q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p
q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p![]() q是n的最佳分解,并規定:F(n)=
q是n的最佳分解,并規定:F(n)=![]() ,例如12可以分解為1
,例如12可以分解為1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因為12-1>6-2>4-3,所以3
4,因為12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一個正整數![]() 是另外一個正整數b的平方,我們稱正整數a是完全平方數,求證:對任意一個完全平方數m,總有F(m)=1
是另外一個正整數b的平方,我們稱正整數a是完全平方數,求證:對任意一個完全平方數m,總有F(m)=1
(2)如果一個兩位正整數t,t=10x+y (1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為18,那么我們就稱這個數t為“吉祥數”,求所有“吉祥數”中F(t)的最大值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】合并下列多項式中的同類項:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣![]() a2b
a2b
查看答案和解析>>
科目:初中數學 來源: 題型:
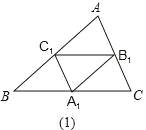
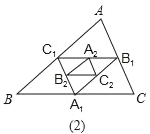
【題目】如圖,在圖(1)中,A1、B1、C1分別是△ABC的邊BC、CA、AB上的點,且A1C1∥AC,A1B1∥AB,B1C1∥BC,在圖(2)中,A2、B2、C2分別是△A1B1C1的邊B1C1、C1A1、A1B1上的點,且A2C2∥A1C1,A2B2∥A1B1,B2C2∥B1C1,…,按此規律,則第n個圖形中平行四邊形的個數共有__個.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com