解:直接應用:
∵函數y=x+

(a>0,x>0),由上述結論可知:當x=

時,該函數有最小值為2

.
∴函數y
1=x(x>0)與函數y
2=

(x>0),則當x=1時,y
1+y
2取得最小值為2.
故答案為:1,2;
變形應用
已知函數y
1=x+1(x>-1)與函數y
2=(x+1)
2+4(x>-1),
則
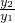
=
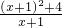
=(x+1)+
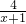
的最小值為:2

=4,
∵當(x+1)+
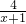
=4時,
整理得出:x
2-2x+1=0,
解得:x
1=x
2=1,
檢驗:x=1時,x+1=2≠0,
故x=1是原方程的解,
故
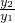
的最小值為4,相應的x的值為1;
實戰演練:
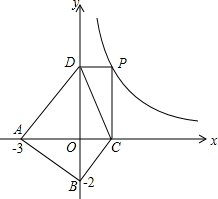
(1)S=S
△AOD+S
△AOB+S
△BOC+S
△DOC,
=

×3×

+

×2×3+

×2×x+

×x×

,
=x+

+6.
故x=3時,最大s的最小=2×3+6=12.
(2)當x=3時,CO=3,DO=

=2,
則DC=
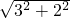
=

,AD=
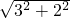
=

,AB=
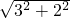
=

,BC=
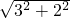
=

,
即DC=AD=AB=BC,
故此時的四邊形ABCD是菱形.
分析:直接運用:可以直接套用題意所給的結論,即可得出結果.
變形運用:先得出
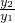
的表達式,然后將(x+1)看做一個整體,繼而再運用所給結論即可.
實戰演練:(1)根據S=S
△AOD+S
△AOB+S
△BOC+S
△DOC,進而求出S與x之間的關系求出最值即可;
(2)利用(1)中所求數據,進而得出DC=AD=AB=BC得出答案即可.
點評:此題考查了反比例函數的應用及幾何不等式的知識和菱形的判定等知識,題目出的比較新穎,解答本題的關鍵是仔細審題,理解題意所給的結論,達到學以致用的目的.

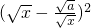 ≥0,所以
≥0,所以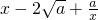 ≥0,從而
≥0,從而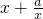 ≥
≥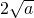 (當
(當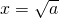 時取等號).設
時取等號).設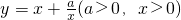 ,由上述結論可知:當
,由上述結論可知:當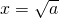 時,y有最小值為
時,y有最小值為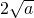 .
. ,則當x=______時,y1+y2取得最小值為______.
,則當x=______時,y1+y2取得最小值為______.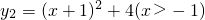 ,求
,求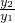 的最小值,并指出取得該最小值時相應的x的值.
的最小值,并指出取得該最小值時相應的x的值. 在第一象限內圖象上的一個動點,過
在第一象限內圖象上的一個動點,過 P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S.
P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S. (a>0,x>0),由上述結論可知:當x=
(a>0,x>0),由上述結論可知:當x= 時,該函數有最小值為2
時,該函數有最小值為2 .
. (x>0),則當x=1時,y1+y2取得最小值為2.
(x>0),則當x=1時,y1+y2取得最小值為2.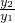 =
=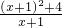 =(x+1)+
=(x+1)+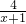 的最小值為:2
的最小值為:2 =4,
=4,
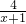 =4時,
=4時,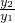 的最小值為4,相應的x的值為1;
的最小值為4,相應的x的值為1; ×3×
×3× +
+ ×2×3+
×2×3+ ×2×x+
×2×x+ ×x×
×x× ,
, +6.
+6. =2,
=2,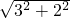 =
= ,AD=
,AD=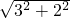 =
= ,AB=
,AB=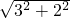 =
= ,BC=
,BC=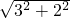 =
= ,
,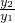 的表達式,然后將(x+1)看做一個整體,繼而再運用所給結論即可.
的表達式,然后將(x+1)看做一個整體,繼而再運用所給結論即可.

 小學教材完全解讀系列答案
小學教材完全解讀系列答案
 P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S.
P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S. ≥0,所以
≥0,所以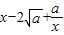 ≥0,從而
≥0,從而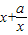 ≥
≥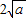 (當
(當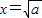 時取等號).設
時取等號).設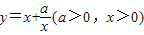 ,由上述結論可知:當
,由上述結論可知:當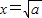 時,y有最小值為
時,y有最小值為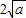 .
.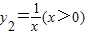 ,則當x=______時,y1+y2取得最小值為______.
,則當x=______時,y1+y2取得最小值為______.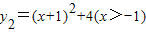 ,求
,求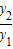 的最小值,并指出取得該最小值時相應的x的值.
的最小值,并指出取得該最小值時相應的x的值.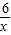 在第一象限內圖象上的一個動點,過
在第一象限內圖象上的一個動點,過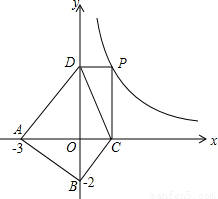 P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S.
P點作PC垂直于x軸,PD垂直于y軸,垂足分別為點C、D.設點P的橫坐標為x,四邊形ABCD的面積為S.