
分析 (1)設該超市購進甲商品x件,則購進乙商品(80-x)件,根據恰好用去1600元,求出x的值,即可得到結果;
(2)設該超市購進甲商品x件,乙商品(80-x)件,根據兩種商品共80件的購進費用不超過1640元,且總利潤(利潤=售價-進價)不少于600元列出不等式組,求出不等式組的解集確定出x的值,即可設計相應的進貨方案,并找出使該超市利潤最大的方案.
解答 解:(1)設該超市購進甲商品x件,則購進乙商品(80-x)件,
根據題意得:10x+30(80-x)=1600,
解得:x=40,
80-x=40,
則購進甲種商品40件、乙種商品40件;
(2)設該超市購進甲商品x件,乙商品(80-x)件,
由題意得:$\left\{\begin{array}{l}{10x+30(80-x)≤1640}\\{5x+10(80-x)≥600}\end{array}\right.$,
解得:38≤x≤40,
∵x為非負整數,
∴x=38,39,40,相應地y=42,41,40,
進而利潤分別為:
5×38+10×42=190+420=610(元),
5×39+10×41=195+410=605(元),
5×40+10×40=200+400=600(元),
則該超市利潤最大的方案是購進甲商品38件,乙商品42件.
點評 此題考查了一元一次不等式組的應用,以及一元一次方程的應用,找出題中的等量關系及不等式關系是解本題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,已知拋物線l1經過原點與A點,其頂點是P(-2,3),平行于y軸的直線m與x軸交于點B(b,0),與拋物線l1交于點M.
如圖,已知拋物線l1經過原點與A點,其頂點是P(-2,3),平行于y軸的直線m與x軸交于點B(b,0),與拋物線l1交于點M.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
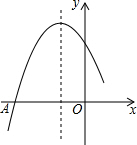 如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論,其中正確結論是( )
如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論,其中正確結論是( )| A. | b2<4ac | |
| B. | 2a+b=0 | |
| C. | a+b+c>0 | |
| D. | 若點B($\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)為函數圖象上的兩點,則y1<y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 測驗 類別 | 平時測驗 | 期中 測驗 | 期末 測驗 | |||
| 第1次 | 第2此 | 第3次 | 第4次 | |||
| 成績 | 80 | 86 | 84 | 90 | 90 | 95 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com