
 如圖,PA、PB是⊙O的切線,A、B為切點,∠OAB=30°,OA=3,則陰影部分面積為9$\sqrt{3}$-3π.
如圖,PA、PB是⊙O的切線,A、B為切點,∠OAB=30°,OA=3,則陰影部分面積為9$\sqrt{3}$-3π. 分析 根據四邊形的內角和為360°,根據切線的性質可知:∠OAP=∠OBP=90°,求出∠AOB的度數,進一步求得∠APB的度數,然后根據陰影部分的面積等于四邊形OAPB的面積減去扇形AOB的面積即可求得.
解答  解:∵在△ABO中,OA=OB,∠OAB=30°,
解:∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°-2×30°=120°,
∵PA、PB是⊙O的切線,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四邊形OAPB中,∠APB=360°-120°-90°-90°=60°.
連接OP.
根據切線長定理得∠APO=30°,
∴OP=2OA=6,AP=OP•cos30°=3$\sqrt{3}$,∠AOP=60°.
∴四邊形的面積=2S△AOP=2×$\frac{1}{2}$×3×3$\sqrt{3}$=9$\sqrt{3}$;扇形的面積是$\frac{120π×{3}^{2}}{360}$=3π,
∴陰影部分的面積是9$\sqrt{3}$-3π.
故答案為9$\sqrt{3}$-3π.
點評 本題考查了切線長定理、切線的性質定理以及30°的直角三角形的性質.關鍵是熟練運用扇形的面積計算公式,能夠把四邊形的面積轉化為三角形的面積計算..


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,OC是∠AOD的平分線,OE是∠BOD的平分線.
如圖所示,OC是∠AOD的平分線,OE是∠BOD的平分線.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m>2,其中正確結論的個數是( )
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m>2,其中正確結論的個數是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知線段AB的長為a,延長線段AB至點C,使BC=$\frac{1}{2}AB$.
如圖,已知線段AB的長為a,延長線段AB至點C,使BC=$\frac{1}{2}AB$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
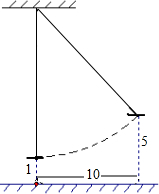 如圖所示,有一架繩索拉直的秋千,當它靜止時,踏板與地面的距離為1尺;將它往前推進10尺,踏板與地面的距離就為5尺.
如圖所示,有一架繩索拉直的秋千,當它靜止時,踏板與地面的距離為1尺;將它往前推進10尺,踏板與地面的距離就為5尺.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com