
【題目】閱讀以下材料:
對數的創始人是蘇格蘭數學家納皮爾(J.Nplcr,1550﹣1617年),納皮爾發明對數是在指數書寫方式之前,直到18世紀瑞士數學家歐拉(Evlcr,1707﹣1783年)才發現指數與對數之間的聯系.
對數的定義:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記作
的對數,記作![]() ,比如指數式
,比如指數式![]() 可以轉化為對數式
可以轉化為對數式![]() ,對數式
,對數式![]() ,可以轉化為指數式
,可以轉化為指數式![]() .
.
我們根據對數的定義可得到對數的一個性質:
![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),理由如下:
),理由如下:
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,由對數的定義得
,由對數的定義得![]()
又∵![]()
∴![]()
根據閱讀材料,解決以下問題:
(1)將指數式![]() 轉化為對數式________;
轉化為對數式________;
(2)求證:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )
)
(3)拓展運用:計算![]() ________.
________.
科目:初中數學 來源: 題型:
【題目】如圖,風車的支桿OE垂直于桌面,風車中心O到桌面的距離OE為25cm,小小風車在風吹動下繞著中心O不停地轉動,轉動過程中,葉片端點A、B、C、D在同一圓O上,已知⊙O的半徑為10cm,
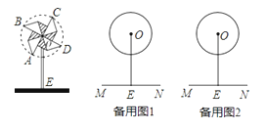
(1)風車在轉動過程中,當∠AOE=30°時,求點A到桌面的距離.
(2)在風車轉動一周的過程中,求點A相對于桌面的高度不超過20cm所經過的路線長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校創客社團計劃利用新購買的無人機設備測量學校旗桿![]() 的高.他們先將無人機放在旗桿前的點
的高.他們先將無人機放在旗桿前的點![]() 處(無人機自身的高度忽略不計),測得此時點
處(無人機自身的高度忽略不計),測得此時點![]() 的仰角為
的仰角為![]() ,因為旗桿底部有臺階,所以不能直接測出垂足
,因為旗桿底部有臺階,所以不能直接測出垂足![]() 到點
到點![]() 的距離.無人機起飛后,被風吹至點
的距離.無人機起飛后,被風吹至點![]() 處,此時無人機距地面的高度為3米,測得此時點
處,此時無人機距地面的高度為3米,測得此時點![]() 的俯角為
的俯角為![]() ,點
,點![]() 的仰角為
的仰角為![]() ,且點
,且點![]() ,
,![]() ,
,![]() 在同一平面內,求旗桿
在同一平面內,求旗桿![]() 的高度.(計算結果精確到0.1米,參考數據:
的高度.(計算結果精確到0.1米,參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
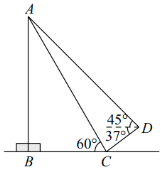
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果三角形的兩個內角α與β滿足2α+β=90°,那么我們稱這樣的三角形為“準互余三角形”.
(1)若△ABC是“準互余三角形”,∠C>90°,∠A=60°,則∠B= °;
(2)如圖①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分線,不難證明△ABD是“準互余三角形”.試問在邊BC上是否存在點E(異于點D),使得△ABE也是“準互余三角形”?若存在,請求出BE的長;若不存在,請說明理由.
(3)如圖②,在四邊形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“準互余三角形”,求對角線AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若拋物線![]() 與
與![]() 軸兩個交點間的距離為2,稱此拋物線為定弦拋物線,已知某定弦拋物線的對稱軸為直線
軸兩個交點間的距離為2,稱此拋物線為定弦拋物線,已知某定弦拋物線的對稱軸為直線![]() ,將此拋物線向下平移3個單位,得到的拋物線過點( )
,將此拋物線向下平移3個單位,得到的拋物線過點( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 、
、![]() 是一次函數
是一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數和一次函數的表達式;
(2)根據圖象寫出使一次函數的函數值小于反比例函數的函數值的x的取值范圍.
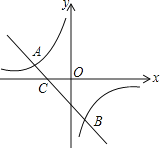
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解下列方程.
(1)(2x+3)2 -16=0
(2)3x2+x-1=0
(3)3x(x-1)=2-2x
(4)9(3x-1)2 =(2-x)2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com