Question

5．把拋物線y=x²-6x向上平移k個單位，新的拋物線頂點坐標為M，與y軸交于點N，P（4，6），當△PMN的面積為20時，則k=$\frac{14}{3}$．

Answer 1

分析 根據平移規律得到新拋物線解析式，易得N的坐標，求直線PN的解析式，表示出與拋物線對稱軸的交點A的坐標，根據頂點M的坐標表示線段AM的長，由三角形的面積公式=鉛直高度×水平距離，進行解答．

解答 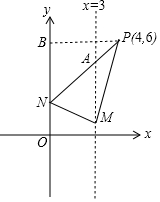解：把拋物線y=x²-6x=（x-3）²-9向上平移k個單位，得到y=（x-3）²-9+k，
則頂點M（3，-9+k），N（0，k），
設PN的解析式為：y=ax+b，
把P（4，6）、N（0，k）代入得：$\left\{\begin{array}{l}{4a+b=6}\\{b=k}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{6-k}{4}}\\{b=k}\end{array}\right.$，
∴PN的解析式為：y=$\frac{6-k}{4}$x+k，
當x=3時，y=$\frac{3（6-k）}{4}$+k=$\frac{1}{4}$k+$\frac{9}{2}$，
∵拋物線的開口向上，
∴拋物線與y軸的交點N總在頂點M的上方，
∴AM=$\frac{1}{4}$k+$\frac{9}{2}$-（-9+k）=-$\frac{3}{4}$k+$\frac{27}{2}$，
過P作PB⊥y軸于B，
∵P（4，6），
∴PB=4，
∵△PMN的面積為20，
∴$\frac{1}{2}$AM•PB=20，
$\frac{1}{2}$（-$\frac{3}{4}$k+$\frac{27}{2}$）×4=20，
k=$\frac{14}{3}$；
故答案為：$\frac{14}{3}$．

點評 本題考查了二次函數的圖象與幾何變換，熟知二次函數圖象的平移法則是解答此題的關鍵，明確上移→+，下移→-，左移→+，右移→-的原則；并注意不規則三角形面積的求法：三角形的面積公式=鉛直高度×水平距離，這在函數的問題中經常運用，要熟練掌握．