
【題目】二次函數![]() (
(![]() )的圖象如圖所示,下列結論:①
)的圖象如圖所示,下列結論:①![]() ;②
;②![]() ;③
;③![]() 為任意實數,則
為任意實數,則![]() ;④
;④![]() ;⑤
;⑤![]() ,其中正確的有( )
,其中正確的有( )
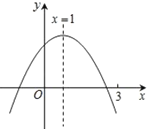
A.①②③B.②④C.②⑤D.②③⑤
【答案】C
【解析】
根據拋物線開口方向得a<0,由拋物線對稱軸為直線x=-![]() =1,得到b=-2a>0,即2a+b=0,由拋物線與y軸的交點位置得到c>0,所以abc<0;根據二次函數的性質得當x=1時,函數有最大值a+b+c,則當m≠1時,a+b+c>am2+bm+c,即a+b>am2+bm;當x=3時函數值小于0,y=9a+3b+c<0,且x=-
=1,得到b=-2a>0,即2a+b=0,由拋物線與y軸的交點位置得到c>0,所以abc<0;根據二次函數的性質得當x=1時,函數有最大值a+b+c,則當m≠1時,a+b+c>am2+bm+c,即a+b>am2+bm;當x=3時函數值小于0,y=9a+3b+c<0,且x=-![]() =1,即b=-2a,從而求得
=1,即b=-2a,從而求得![]() .
.
∵拋物線開口向下,
∴a<0,
∵拋物線對稱軸為直線x=-![]() =1,
=1,
∴b=-2a>0,即2a+b=0,所以②正確;
∵拋物線與y軸的交點在x軸上方,
∴c>0,
∴abc<0,所以①錯誤;
∵拋物線對稱軸為直線x=1,
∴函數的最大值為a+b+c,
∴當m≠1時,a+b+c>am2+bm+c,即a+b>am2+bm,所以③錯誤;
∵拋物線與x軸的一個交點在(3,0)的左側,而對稱軸為直線x=1,
∴拋物線與x軸的另一個交點在(-1,0)的右側
∴當x=-1時,y<0,
∴a-b+c<0,所以④錯誤;
當x=3時函數值小于0,y=9a+3b+c<0,且x=-![]() =1,
=1,
即b=-2a,代入得9a+6a+c<0,得![]() ,所以⑤正確.
,所以⑤正確.
綜上所述,正確的有②⑤.
故選C.


科目:初中數學 來源: 題型:
【題目】請閱讀下列材料:
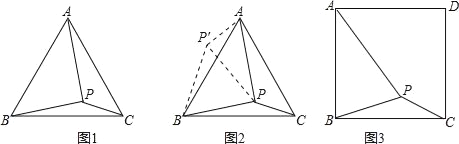
問題:如圖1,在等邊三角形ABC內有一點P,且PA=2,PB=![]() ,PC=1、求∠BPC度數的大小和等邊三角形ABC的邊長.
,PC=1、求∠BPC度數的大小和等邊三角形ABC的邊長.
小剛同學的思路是:將△BPC繞點B逆時針旋轉60°,畫出旋轉后的圖形(如圖2),連接PP′,可得△P′PC是等邊三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可證),所以∠APB=150°,而∠BPC=∠AP′B=150°,進而求出等邊△ABC的邊長為![]() ,問題得到解決.
,問題得到解決.
請你參考小剛同學的思路,探究并解決下列問題:
如圖3,在正方形ABCD內有一點P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度數的大小和正方形ABCD的邊長.
.求∠BPC度數的大小和正方形ABCD的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班數學興趣小組經過市場調查,整理出某種商品在第![]() 天的售價與銷量的相關信息如下表:
天的售價與銷量的相關信息如下表:
觀察表格:根據表格解答下列問題:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
(2)在下圖的直角坐標系中畫出函數![]() 的圖象,并根據圖象,直接寫出當
的圖象,并根據圖象,直接寫出當![]() 取什么實數時,不等式
取什么實數時,不等式![]() 成立;
成立;
(3)該圖象與![]() 軸兩交點從左到右依次分別為
軸兩交點從左到右依次分別為![]() 、
、![]() ,與
,與![]() 軸交點為
軸交點為![]() ,求過這三個點的外接圓的半徑.
,求過這三個點的外接圓的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
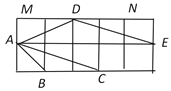
【題目】如圖,在2×2的正方形網格中,小正方形的邊長均為1,△ABC與△ADE的頂點都在格點上.
(1)求證:△ABC∽△ADE;
(2)求∠MDA+∠NDE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
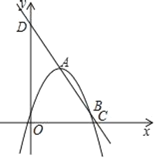
【題目】如圖所示,二次函數y=k(x﹣1)2+2的圖象與一次函數y=kx﹣k+2的圖象交于A、B兩點,點B在點A的右側,直線AB分別與x、y軸交于C、D兩點,其中k<0.
(1)求A、B兩點的橫坐標;
(2)若△OAB是以OA為腰的等腰三角形,求k的值;
(3)二次函數圖象的對稱軸與x軸交于點E,是否存在實數k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
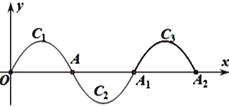
【題目】如圖,一段拋物線:y=-x(x-2)(0≤x≤2)記為C1 ,它與x軸交于兩點O,A;將C1繞點A旋轉180°得到C2 , 交x軸于A1;將C2繞點A1旋轉180°得到C3 , 交x軸于點A2 . .....如此進行下去,直至得到C2018 , 若點P(4035,m)在第2018段拋物線上,則m的值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c 如圖所示,直線x=-1是其對稱軸,

(1)確定a,b,c, Δ=b2-4ac的符號,
(2)求證:a-b+c>0,
(3)當x取何值時,y>0;當x取何值時y<0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com