
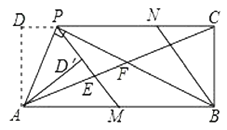
【題目】在矩形![]() 中,
中,![]() 為
為![]() 邊上一點
邊上一點![]() ,
,![]() .將
.將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延長線交邊
的延長線交邊![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .連接
.連接![]() ,分別交
,分別交![]() ,
,![]() 于點
于點![]() ,
,![]() .現有以下結論:①連接
.現有以下結論:①連接![]() ,則
,則![]() 垂直平分
垂直平分![]() ;②四邊形
;②四邊形![]() 是菱形;③
是菱形;③![]() ;④若
;④若![]() ,則
,則![]() .其中正確的結論是________(填寫所有正確結論的序號).
.其中正確的結論是________(填寫所有正確結論的序號).
【答案】①②③
【解析】
①連接![]() ,根據翻折的性質,結合等腰三角形三線合一的性質即可得出結論;
,根據翻折的性質,結合等腰三角形三線合一的性質即可得出結論;
②DP∥AB,所以∠DPA=∠PAM,由題意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB-∠PAM=∠APB-∠APM,即∠ABP=∠MPB,從而可知PM=MB=AM,又易證四邊形PMBN是平行四邊形,所以四邊形PMBN是菱形;
③過點P作PG⊥AB于點G,易知四邊形DPGA,四邊形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易證△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
④由于![]() ,可設DP=1,AD=2,由(1)可知:AG=DP=1,PG=AD=2,從而求出GB=PC=4,AB=AG+GB=5,由于CP∥AB,從而可證△PCF∽△BAF,△PCE∽△MAE,從而可得
,可設DP=1,AD=2,由(1)可知:AG=DP=1,PG=AD=2,從而求出GB=PC=4,AB=AG+GB=5,由于CP∥AB,從而可證△PCF∽△BAF,△PCE∽△MAE,從而可得![]() ,
,![]() ,從而可求出EF=AF-AE=
,從而可求出EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,從而可得
AC,從而可得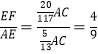 .
.
①根據翻折的性質可得,AD=A![]() ,∠DAP=∠
,∠DAP=∠![]() AP,
AP,
連接![]() ,根據等腰三角形“三線合一”的性質得,
,根據等腰三角形“三線合一”的性質得,![]() 垂直平分
垂直平分![]() .
.
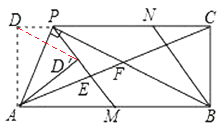
②∵DP∥AB,
∴∠DPA=∠PAM,
由題意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB-∠PAM=∠APB-∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
又易證四邊形PMBN是平行四邊形,
∴四邊形PMBN是菱形;
③過點P作PG⊥AB于點G,
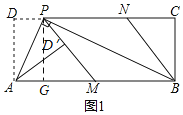
∴易知四邊形DPGA,四邊形PCBG是矩形,
∴AD=PG,DP=AG,GB=PC
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() ,
,
∴PG2=AGGB,
即AD2=DPPC;
④由于![]() ,
,
可設DP=1,AD=2,
由(1)可知:AG=DP=1,PG=AD=2,
∵PG2=AGGB,
∴4=1GB,
∴GB=PC=4,
AB=AG+GB=5,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() ,
,
∴![]() ,
,
又易證:△PCE∽△MAE,AM=![]() AB=
AB=![]() ,
,
∴![]()
∴![]() ,
,
∴EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,
AC,
∴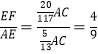 .
.
故答案為:①②③.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,與x軸的另一個交點為C,頂點為D,連結CD.
兩點,與x軸的另一個交點為C,頂點為D,連結CD.
(1)求該拋物線的表達式;
(2)點P為該拋物線上一動點(與點B、C不重合),設點P的橫坐標為t.
①當點P在直線BC的下方運動時,求![]() 的面積的最大值;
的面積的最大值;
②該拋物線上是否存在點P,使得![]() 若存在,求出所有點P的坐標;若不存在,請說明理由.
若存在,求出所有點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
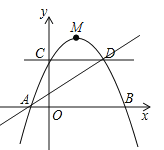
【題目】如圖,已知頂點為![]() 的拋物線過點
的拋物線過點![]() ,交
,交![]() 軸于
軸于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,點
,點![]() 是拋物線上一動點.
是拋物線上一動點.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 當點
當點![]() 在直線
在直線![]() 上方時,求
上方時,求![]() 面積的最大值,并求出此時點
面積的最大值,并求出此時點![]() 的坐標;
的坐標;
![]() 過點
過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,若將
,若將![]() 沿
沿![]() 翻折點
翻折點![]() 的對應點為點
的對應點為點![]() .是否存在點
.是否存在點![]() ,使
,使![]() 恰好落在
恰好落在![]() 軸上?若存在,求出點
軸上?若存在,求出點![]() 的坐標:若不存在,說明理由.
的坐標:若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點P在BC上.
(1)求作:△PCD,使點D在AC上,且△PCD∽△ABP;(要求:尺規作圖,保留作圖痕跡,不寫作法)
(2)在(1)的條件下,若∠APC=2∠ABC,求證:PD//AB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了落實黨的“精準扶貧”政策,A、B兩城決定向C,D兩鄉運送肥料以支持農村生產,已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉運肥料的費用分別為20元/噸和25元/噸:從B城往C,D兩鄉運肥料的費用分別為15元/噸和24元/噸,現C鄉需要肥料240噸,D鄉需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設從A城運往C鄉肥料x噸,總運費為y元,求y與x的函數關系式.
(3)怎樣調運才能使總運費最少?并求最少運費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
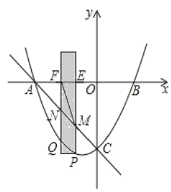
的坐標為![]() .有一寬度為1,長度足夠長的矩形(陰影部分)沿
.有一寬度為1,長度足夠長的矩形(陰影部分)沿![]() 軸方向平移,與
軸方向平移,與![]() 軸平行的一組對邊交拋物線于點
軸平行的一組對邊交拋物線于點![]() 和點
和點![]() ,交直線
,交直線![]() 于點
于點![]() 和點
和點![]() ,交
,交![]() 軸于點
軸于點![]() 和點
和點![]() .
.
(1)求拋物線的解析式及點![]() 的坐標;
的坐標;
(2)當點![]() 和
和![]() 都在線段
都在線段![]() 上時,連接
上時,連接![]() ,如果
,如果![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在矩形的平移過程中,是否存在以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,若存在,求出點
為頂點的四邊形是平行四邊形,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
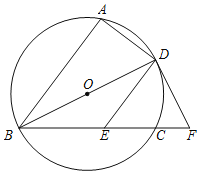
【題目】如圖,![]() ,
,![]() ,
,![]() 三點在
三點在![]() 上,直徑
上,直徑![]() 平分
平分![]() ,過點
,過點![]() 作
作![]() 交弦
交弦![]() 于點
于點![]() ,在
,在![]() 的延長線上取一點
的延長線上取一點![]() ,使得
,使得![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)連接AF交DE于點M,若AD=4,DE=5,求DM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某中心廣場燈柱AB被鋼纜CD固定,已知CB=5米,且sin∠DCB=![]() .
.
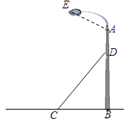
(1)求鋼纜CD的長度。
(2)若AD=2米,燈的頂端E距離A處1.6米,且∠EAB=120°,則燈的頂端E距離地面多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年3月25日是第二十四個“全國中小學生安全教育日”,某校為加強學生的安全意識,以“防火、防溺水、防食物中毒、防校園欺凌”為主題組織了全校學生參加安全知識競賽,從中抽取了部分學生成績(得分為正整數,滿分為100分)進行統計,繪制了兩幅不完整的統計圖,如圖所示.
(1)學校共抽取了______名學生,![]() _____,n=______.
_____,n=______.
(2)補全頻數直方圖;
(3)該校共有2000名學生。若成績在70分以下(含70分)的學生安全意識不強,有待進一步加強安全教育,則該校安全意識不強的學生約有多少人?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com