
已知:如圖,四邊形ABCD為平行四邊形,以CD為直徑作⊙O,⊙O與邊BC相交于點F,⊙O的切線DE與邊AB相交于點E,且AE=3EB.
(1)求證:△ADE∽△CDF;
(2)當CF:FB=1:2時,求⊙O與▱ABCD的面積之比.
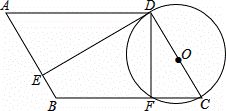
(1)證明 :∵CD是⊙O的直徑,
:∵CD是⊙O的直徑,
∴∠DFC=90°,
∵四邊形ABCD是平行四邊形,
∴∠A=∠C,AD∥BC,
∴∠ADF=∠DFC=90°,
∵DE為⊙O的切線,
∴DE⊥DC,
∴∠EDC=90°,
∴∠ADF=∠EDC=90°,
∴∠ADE=∠CDF,
∵∠A=∠C,
∴△ADE∽△CDE;
(2)解:∵CF:FB=1:2,
∴設CF=x,FB=2x,則BC=3x,
∵AE=3EB,
∴設EB=y,則AE=3y,AB=4y,
∵四邊形ABCD是平行四邊形,
∴AD=BC=3x,AB=DC=4y,
∵△ADE∽△CDF,
∴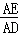 =
=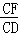 ,
,
∴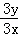 =
= ,
,
∵x、y均為正數,
∴x=2y,
∴BC=6y,CF=2y,
在Rt△DFC中,∠DFC=90°,
由勾股定理得:DF=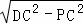 =
=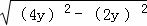 =2
=2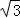 y,
y,
∴⊙O的面積為π•( DC)2=
DC)2=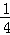 π•DC2=
π•DC2=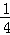 π(4y)2=4πy2,
π(4y)2=4πy2,
四邊形ABCD的面積為BC•DF=6y•2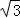 y=12
y=12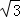 y2,
y2,
∴⊙O與四邊形ABCD的面積之比為4πy2:12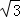 y2=π:3
y2=π:3 .
.


科目:初中數學 來源: 題型:
甲、乙、丙三位同學進行報數游戲,游戲規則為:甲報1,乙報2,丙報3,再甲報4,乙報5,丙報6,…依次循環反復下去,當報出的數為2014時游戲結束,若報出的數是偶數,則該同學得1分.當報數結束時甲同學的得分是 分.
查看答案和解析>>
科目:初中數學 來源: 題型:
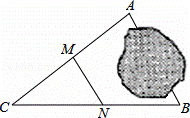
如圖,A,B兩地被池塘隔開,小明通過下列方法測出了A、B間的距離:先在AB外選一點C,然后測出AC,BC的中點M,N,并測量出MN的長為12m,由此他就知道了A、B間的距離.有關他這次探究活動的描述錯誤的是( )
|
| A. | AB=24m | B. | MN∥AB | C. | △CMN∽△CAB | D. | CM:MA=1:2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
為促進義務教育辦學條件均衡,某市投入480萬元資金為部分學校添置實驗儀器及音、體、美器材,480萬元用科學記數法表示為( )
| A. | 480×104元 | B. | 48×105元 | C. | 4.8×106元 | D. | 0.48×107元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com