
【題目】我們知道:有兩條邊相等的三角形叫做等腰三角形.類似地,我們定義:至少有一組對邊相等的四邊形叫做等對邊四邊形.
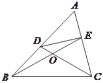
(1)如圖,在![]() 中,點
中,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,設
上,設![]() ,
,![]() 相交于點
相交于點![]() ,若
,若![]() ,
,![]() .請你寫出圖中一個與
.請你寫出圖中一個與![]() 相等的角,并猜想圖中哪個四邊形是等對邊四邊形?
相等的角,并猜想圖中哪個四邊形是等對邊四邊形?
(2)在![]() 中,如果
中,如果![]() 是不等于
是不等于![]() 的銳角,點
的銳角,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() .探究:滿足上述條件的圖形中是否存在等對邊四邊形,并證明你的結論.
.探究:滿足上述條件的圖形中是否存在等對邊四邊形,并證明你的結論.
【答案】(1)與∠A相等的角是∠BOD、∠COE,四邊形DBCE是等對邊四邊形;(2)存在等對邊四邊形DBCE,證明見解析;
【解析】
(1)根據三角形外角的性質可得∠BOD=60°,根據對頂角的性質可得∠COE=60°;作CG⊥BE于G點,作BF⊥C,D交CD延長線于F點通過證明△BCF≌△CBG,可得BF=CG,,再證明△BDF≌△CEG,即可證明四邊形DBCE是等對邊四邊形;
(2)作CG⊥BE于G點,作BF⊥CD交CD延長線于F點.易證△BCF≌△CBG,進而證明△BDF≌△CEG,所以BD=CE,所以四邊形DBCE是等對邊四邊形.
(1)∵∠A=60°,![]()
∴∠OBC=∠OCB=30°
∴∠BOD=∠COE=∠OBC+∠OCB=30°+30°=60°,
∴與∠A相等的角是∠BOD、∠COE,
四邊形DBCE是等對邊四邊形,證明如下:
如圖,作CG⊥BE于G點,作BF⊥CD交CD延長線于F點.
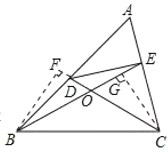
∴∠BFC=∠CGB=∠CGE=90°
∵∠DCB=∠EBC=![]() ∠A,BC=BC,
∠A,BC=BC,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠DOB,∠BEC=∠ABE+∠A,∠A=∠BOD
∴∠BDF=∠BEC,
又∵∠BFD=∠CGE=90°,BF=CG,
∴△BDF≌△CEG,
∴BD=CE,
∴四邊形DBCE是等對邊四邊形.
(2)存在等對邊四邊形DBCE,理由如下:
如圖,作CG⊥BE于G點,作BF⊥CD交CD延長線于F點.

∴∠BFC=∠CGB=∠CGE=90°
∵∠DCB=∠EBC=![]() ∠A,BC=BC,
∠A,BC=BC,
∴△BCF≌△CBG,
∴BF=CG,
∵![]()
∴∠BOD =∠OBC+∠OCB=![]() ,
,
∴∠A=∠BOD,
∵∠BDF=∠ABE+∠DOB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
又∵∠BDF=∠CGE=90°,BF=CG,
∴△BDF≌△CEG,
∴BD=CE,
∴四邊形DBCE是等對邊四邊形.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:初中數學 來源: 題型:
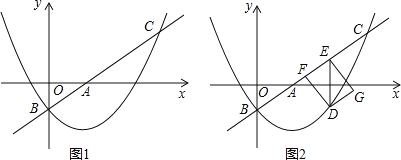
【題目】如圖1,在平面直角坐標系![]() 中,直線
中,直線![]() 與x軸、y軸分別交于點A和點B(0,-1),拋物線
與x軸、y軸分別交于點A和點B(0,-1),拋物線![]() 經過點B,且與直線l的另一個交點為C(4,n).
經過點B,且與直線l的另一個交點為C(4,n).
(1)求n的值和拋物線的解析式;
(2)點D在拋物線上,且點D的橫坐標為t(0<t<4),DE∥y軸交直線l于點E,點F在直線l上,且四邊形DFEG為矩形(如圖2).若矩形DFEG的周長為p,求p與t的函數關系式以及p的最大值;
(3)M是平面內一點,將△AOB繞點M沿逆時針方向旋轉90°后,得到△A'O'B',點A、O、B的對應點分別是點A'、O'、B'. 若△A'O'B'的兩個頂點恰好落在拋物線上,請直接寫出點A’的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平行四邊形![]() 中,
中, ![]() ,垂足為
,垂足為![]() 與
與![]() 的延長線相交于
的延長線相交于![]() ,且
,且![]() ,連接
,連接![]() ;
;
(1)如圖![]() ,求證:四邊形
,求證:四邊形![]() 是菱形;
是菱形;
(2)如圖![]() ,連接
,連接![]() ,若
,若![]() ,在不添加任何輔助線的情況下,直接寫出圖
,在不添加任何輔助線的情況下,直接寫出圖![]() 中所有面積等于
中所有面積等于![]() 的面積的鈍角三角形.
的面積的鈍角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
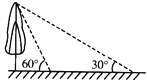
【題目】如圖,校園內有一棵與地面垂直的樹,數學興趣小組兩次測量它在地面上的影子,第一次是陽光與地面成60°角時,第二次是陽光與地面成30°角時,兩次測量的影長相差8米,則樹高_____________米(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著襄陽市近幾年城市建設的快速發展,對花木的需求量逐年提高.某園林專業戶計劃投資種植花卉及樹木,根據市場調查與預測,種植樹木的利潤![]() 與投資量
與投資量![]() 成正比例關系,如圖1所示;種植花卉的利潤
成正比例關系,如圖1所示;種植花卉的利潤![]() 與投資量
與投資量![]() 成二次函數關系,如圖2所示(注:利潤與投資量的單位:萬元)
成二次函數關系,如圖2所示(注:利潤與投資量的單位:萬元)
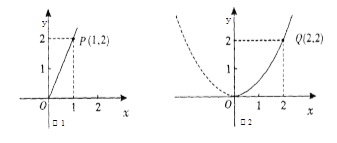
(1)分別求出利潤![]() 與
與![]() 關于投資量
關于投資量![]() 的函數關系式;
的函數關系式;
(2)如果這位專業戶以10萬元資金投入種植花卉和樹木,求他獲得的最大利潤是多少?
(3)在(2)的條件下,根據對市場需求的調查,這位專業戶決定投入種植樹木的資金不得高于投入種植花卉的資金,他至少獲得多少利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學家吳文俊院士非常重視古代數學家賈憲提出的“從長方形對角線上任一點作兩條分別平行于兩鄰邊的直線,則所容兩長方形面積相等(如圖所示)”這一推論,他從這一推論出發,利用“出入相補”原理復原了《海島算經》九題古證,根據圖形可知他得出的這個推論指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一邊是另一邊的![]() 倍的三角形叫做智慧三角形,這兩邊中較長邊稱為智慧邊,這兩邊的 夾角叫做智慧角.
倍的三角形叫做智慧三角形,這兩邊中較長邊稱為智慧邊,這兩邊的 夾角叫做智慧角.
(1)在 Rt△ABC 中,∠ACB=90°,若∠A 為智慧角,則∠B 的度數為 ;
(2)如圖①,在△ABC 中,∠A=45°,∠B=30°,求證:△ABC 是智慧三角形;
(3)如圖②,△ABC 是智慧三角形,BC 為智慧邊,∠B 為智慧角,A(3,0),點 B,C 在函數 y=![]() (x>0)的圖像上,點 C 在點 B 的上方,且點 B 的縱坐標為
(x>0)的圖像上,點 C 在點 B 的上方,且點 B 的縱坐標為![]() .當△ABC是直角三角形時,求 k 的值.
.當△ABC是直角三角形時,求 k 的值.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一條單車道的拋物線形隧道如圖所示.隧道中公路的寬度AB=8m,隧道的最高點C到公路的距離為6m.
(1)建立適當的平面直角坐標系,求拋物線的表達式;
(2)現有一輛貨車的高度是4.4m,貨車的寬度是2m,為了保證安全,車頂距離隧道頂部至少0.5m,通過計算說明這輛貨車能否安全通過這條隧道.
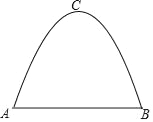
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com