
【題目】在平面直角坐標系的網格中,橫、縱坐標均為整數的點叫做格點,例如:![]() ,
,![]() ,
,![]() ,
,![]() 都是格點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖保留連線的痕跡,不要求說明理由.
都是格點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖保留連線的痕跡,不要求說明理由.
(1)若點![]() 為格點,以點
為格點,以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是軸對稱圖形,在圖1中畫出所有符合題意的四邊形,并寫出點
為頂點的四邊形是軸對稱圖形,在圖1中畫出所有符合題意的四邊形,并寫出點![]() 的坐標以及四邊形的面積;
的坐標以及四邊形的面積;

(2)如圖2,在線段![]() 上畫點
上畫點![]() ,使得
,使得![]() .
.

 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】已知,如圖,∠B=∠C=90 ,M是BC的中點,DM平分∠ADC.

(1)若連接AM,則AM是否平分∠BAD?請你證明你的結論;
(2)線段DM與AM有怎樣的位置關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),在平面直角坐標系中,四邊形OABC的頂點O是坐標原點,點A坐標(6,0),點B在y軸上,點C在第三象限角平分線上,動點P、Q同時從點O出發,點P以1cm/s 的速度沿O→A→B勻速運動到終點B;點Q沿O→C→B→A運動到終點A,點Q在線段OC、CB、BA上分別作勻速運動,速度分別為V1cm/s、V2cm/s、V3cm/s.設點P運動的時間為t(s),△OPQ的面積為S(cm2),已知S與t之間的部分函數關系如圖(2)中的曲線段OE、曲線段EF和線段FG所示.
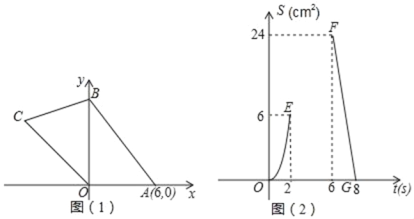
(1)V1= ,V2= ;
(2)求曲線段EF的解析式;
(3)補全函數圖象(請標注必要的數據);
(4)當點P、Q在運動過程中是否存在這樣的t,使得直線PQ把四邊形OABC的面積分成11:13兩部分,若存在直接寫出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠C=120°,AD=2AB=4,點H、G分別是邊CD、BC上的動點.連接AH、HG,點E為AH的中點,點F為GH的中點,連接EF.則EF的最大值與最小值的差為( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的6月5日為世界環保日,為了提倡低碳環保,某公司決定購買10臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購. 經調查:購買3臺甲型設備比購買2臺乙型設備多花16萬元,購買2臺甲型設備比購買3臺乙型設備少花6萬元.
(1)求甲、乙兩種型號設備的價格;
(2)該公司經預算決定購買節省能源的新設備的資金不超過110萬元,你認為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設備的產量為240噸/月,乙型設備的產量為180噸/月.若每月要求總產量不低于2040噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)我們已經知道,在![]() 中,如果
中,如果![]() ,則
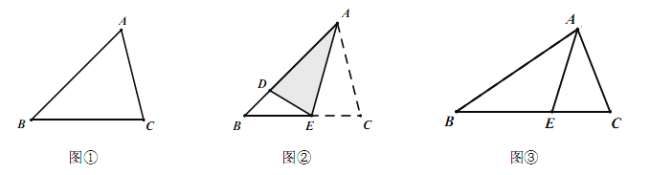
,則![]() ,下面我們繼續研究:如圖①,在
,下面我們繼續研究:如圖①,在![]() 中,如果
中,如果![]() ,則
,則![]() 與
與![]() 的大小關系如何?為此,我們把
的大小關系如何?為此,我們把![]() 沿
沿![]() 的平分線翻折,因為
的平分線翻折,因為![]() ,所以點
,所以點![]() 落在
落在![]() 邊的點
邊的點![]() 處,如圖②所示,然后把紙展平,連接
處,如圖②所示,然后把紙展平,連接![]() ,接下來,你能推出
,接下來,你能推出![]() 與
與![]() 的大小關系了嗎?試寫出說理過程.
的大小關系了嗎?試寫出說理過程.
(2)如圖③,在![]() 中,
中,![]() 是角平分線,且
是角平分線,且![]() ,求證:
,求證:![]() .
.
(3)在(2)的條件下,若點![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的動點,且
上的動點,且![]() ,
,![]() ,則
,則![]() 的最小值為 .
的最小值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數y1=x﹣m+1和y2=![]() (n≠0)的圖象交于P,Q兩點.
(n≠0)的圖象交于P,Q兩點.
(1)若y1的圖象過(n,0),且m+n=3,求y2的函數表達式:
(2)若P,Q關于原點成中心對稱.
①求m的值;
②當x>2時,對于滿足條件0<n<n0的一切n總有y1>y2,求n0的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com