【題目】已知拋物線y＝﹣x2+bx+c經過點A（﹣1，0），與y軸交于點B，且對稱軸為x＝1．
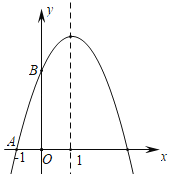
（1）求該拋物線的解析式；
（2）點P是拋物線對稱軸上的一動點，當|PA﹣PB|取最大值時，求點P的坐標．
【答案】（1）y＝﹣x2+2x+3；（2）P（1，6）
【解析】
（1）利用待定系數法即可求得；
（2）根據三角形兩邊之差小于第三邊，得，當點P在直線AB上時，|PA﹣PB|最大，根據△ABO∽△APH求得PH的長度，即可求得P的坐標．
（1）由題意得：
，解得
，
∴該拋物線的解析式：y＝﹣x2+2x+3；
（2）∵拋物線為y＝﹣x2+2x+3，
令x＝0，則y＝3，
∴B（0，3），
∵三角形兩邊之差小于第三邊，
∴當點P在直線AB上時，|PA﹣PB|最大.
設拋物線的對稱軸直線x＝1與x軸交于點H，與直線AB交于點P，
∵PH∥y軸，
∴△ABO∽△APH
∴
，
∴PH＝2BO＝6，
∴P（1，6）即為所求．
名牌學校分層周周測系列答案
黃岡海淀全程培優測試卷系列答案科目：初中數學 來源： 題型：
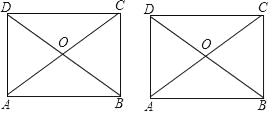
【題目】如圖，已知矩形ABCD，AB＝6，AD＝2
，對角線AC，BD交于點O，E為對角線AC上一點．
（1）求證：△OBC是等邊三角形；
（2）連結BE，當BE＝
時，求線段AE的長；
（3）在BC邊上取點F，設P，Q分別為線段AE，BF的中點，連結EF，PQ．若EF＝2，求PQ的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】評價組對某區九年級教師的試卷講評課的學生參與度進行評價調查，其評價項目為主動質疑、獨立思考、專注聽講、講解題目四項．評價組隨機抽取了若干名同學的參與情況，繪制成如圖所示的扇形統計圖和條形統計圖（均不完整），請根據圖中所給信息解答下列問題：
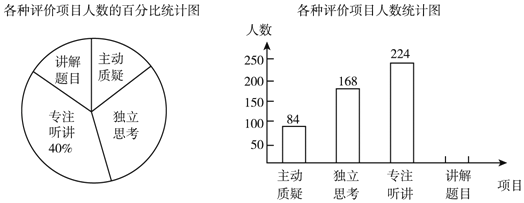
(1)在這次評價中，一共抽查了 名同學；
(2)請將條形統計圖補充完整；
(3)如果全區有6000名九年級學生，那么在試卷評講課中，“獨立思考”的約有多少人？
(4)根據統計反映的情況，請你對該區的九年級同學提出一條對待試卷講評課的建議．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以AD為直徑的半圓O經過Rt△ABC斜邊AB的兩個端點，交直角邊AC于點E；B、E是半圓弧的三等分點，
的長為
，則圖中陰影部分的面積為（ ）
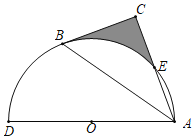
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
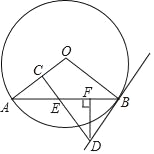
【題目】如圖，AB是⊙O的一條弦，E是AB的中點，過點E作EC⊥OA于點C，過點B作⊙O的切線交CE的延長線于點D．
（1）求證：DB=DE；
（2）若AB=12，BD=5，過D點作DF⊥AB于點F，
①則cos∠EDF= ；
②求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線
與x軸、y軸分別交于A、B兩點，P是以C（0，1）為圓心，1為半徑的圓上一動點，連結PA、PB．則△PAB面積的最大值是（ ）
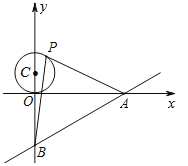
A.8B.12C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
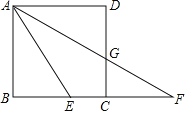
【題目】如圖，點E是正方形ABCD的邊BC上一點，連接AE，將線段AE繞點E順時針旋轉一定的角度得到EF，點C在EF上，連接AF交邊CD于點G．
（1）若AB＝4，BF＝8，求CE的長；
（2）求證：AE＝BE+DG．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠B
90°，AB
4，BC
2，以AC為邊作△ACE，∠ACE
90°，AC=CE，延長BC至點D，使CD
5，連接DE．求證：△ABC∽△CED．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com