
【題目】在研究反比例函數![]() 的圖象與性質時,我們對函數解析式進行了深入分析.
的圖象與性質時,我們對函數解析式進行了深入分析.
首先,確定自變量![]() 的取值范圍是全體非零實數,因此函數圖象會被
的取值范圍是全體非零實數,因此函數圖象會被![]() 軸分成兩部分;其次,分析解析式,得到
軸分成兩部分;其次,分析解析式,得到![]() 隨
隨![]() 的變化趨勢:當
的變化趨勢:當![]() 時,隨著
時,隨著![]() 值的增大,
值的增大,![]() 的值減小,且逐漸接近于零,隨著
的值減小,且逐漸接近于零,隨著![]() 值的減小,
值的減小,![]() 的值會越來越大…,由此,可以大致畫出
的值會越來越大…,由此,可以大致畫出![]() 在
在![]() 時的部分圖象,如圖所示:
時的部分圖象,如圖所示:
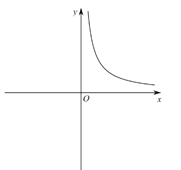
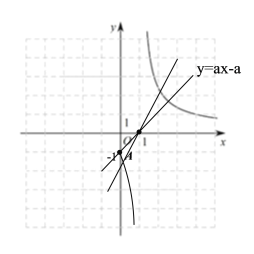
利用同樣的方法,我們可以研究函數![]() 的圖象與性質.通過分析解析式畫出部分函數圖象如圖所示.
的圖象與性質.通過分析解析式畫出部分函數圖象如圖所示.
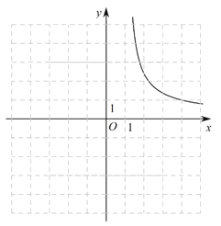
(1)請沿此思路在圖中完善函數圖象的草圖并標出此函數圖象上橫坐標為0的點![]() ;(畫出網格區域內的部分即可)
;(畫出網格區域內的部分即可)
(2)觀察圖象,寫出該函數的一條性質:__________;
(3)若關于![]() 的方程
的方程![]() 有兩個不相等的實數根,結合圖象,直接寫出實數
有兩個不相等的實數根,結合圖象,直接寫出實數![]() 的取值范圍: __________.
的取值范圍: __________.
【答案】(1)見解析;(2)當![]() 時,
時,![]() 隨
隨![]() 增大而減小;(3)
增大而減小;(3)![]()
【解析】
(1)先得出函數![]() 自變量
自變量![]() 的取值范圍,再分析解析式,得到
的取值范圍,再分析解析式,得到![]() 隨
隨![]() 的變化趨勢,由此完善函數圖象即可;令
的變化趨勢,由此完善函數圖象即可;令![]() 求出y的值即可得出點A坐標;
求出y的值即可得出點A坐標;
(2)根據函數圖象得出其增減性即可;
(3)將所求問題看成函數![]() 與一次函數
與一次函數![]() 的交點問題,先找出一個臨界位置,再根據一次函數的性質即可得.
的交點問題,先找出一個臨界位置,再根據一次函數的性質即可得.
(1)由二次根式的被開方數的非負性、分式的分母不能為0得: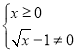
解得:![]() 且
且![]()
令![]() 得
得![]()
則點A坐標為![]()
分析解析式,得到![]() 隨
隨![]() 的變化趨勢:當
的變化趨勢:當![]() 時,隨著
時,隨著![]() 值的增大,
值的增大,![]() 的值會越來越小;當
的值會越來越小;當![]() 時,隨著
時,隨著![]() 值的增大,
值的增大,![]() 的值會減小,且逐漸接近于零,由此,完善函數圖象如圖所示:
的值會減小,且逐漸接近于零,由此,完善函數圖象如圖所示:
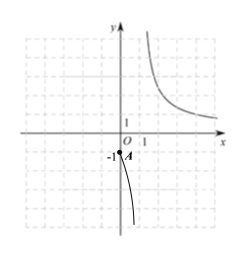
(2)由(1)圖象可知,當![]() 時,
時,![]() 隨
隨![]() 增大而減小;(注:答案不唯一)
增大而減小;(注:答案不唯一)
(3)由題意得,函數![]() 與一次函數
與一次函數![]() 有兩個交點
有兩個交點
一次函數![]() 的圖象經過定點
的圖象經過定點![]()
要使兩個函數有兩個交點,一次函數![]() 經過點
經過點![]() 是一個臨界位置,此時有
是一個臨界位置,此時有![]() ,即
,即![]()
因此,結合函數圖象可知,當![]() 時,兩個函數必有兩個交點,即關于
時,兩個函數必有兩個交點,即關于![]() 的方程
的方程![]() 有兩個不相等的實數根
有兩個不相等的實數根
故答案為:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,過點A作AE⊥BC,垂足為E,連接DE,F為線段DE上一點,且∠AFE=∠B

(1)求證:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的長.
,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
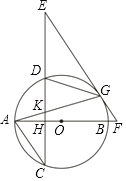
【題目】如圖,AB是⊙O的直徑,過圓外一點E作EF與⊙O相切于G,交AB的延長線于F,EC⊥AB于H,交⊙O于D,C兩點,連接AG交DC于K.
(1)求證:EG=EK;
(2)連接AC,若AC∥EF,cosC=![]() ,AK=
,AK=![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
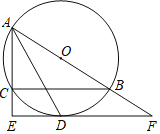
【題目】如圖,⊙O是△ABC的外接圓,AB為直徑,∠BAC的平分線交⊙O于點D,過點D作DE⊥AC分別交AC的延長線于點E,交AB的延長線于點F.
(1)求證:EF是⊙O的切線;
(2)若AC=8,CE=4,求弧BD的長.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是娜娜設計的“作一個角等于已知角”的尺規作圖過程.
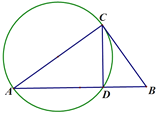
已知:RT△ABC,
求作:AB上作點D,使∠BCD=∠A.

作法:如圖,以AC為直徑作圓,交AB于D,所以點D就是所求作的點;
根據娜娜設計的作圖過程,完成下面的證明.
證明:∵AC是直徑
∴∠ADC=90°(______)(填推理的依據)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分8分)某商家預測一種應季襯衫能暢銷市場,就用13200元購進了一批這種襯衫,面市后果然供不應求.商家又用28800元購進了第二批這種襯衫,所購數量是第一批購進量的2倍,但單價貴了10元.
(1)該商家購進的第一批襯衫是多少件?
(2)若兩批襯衫按相同的標價銷售,最后剩下50件按八折優惠賣出,如果兩批襯衫全部售完后利潤率不低于25%(不考慮其它因素),那么每件襯衫的標價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鄂爾多斯市某百貨商場銷售某一熱銷商品A,其進貨和銷售情況如下:用16000元購進一批該熱銷商品A,上市后很快銷售一空,根據市場需求情況,該商場又用7500元購進第二批該商品,已知第二批所購件數是第一批所購件數的一半,且每件商品的進價比第一批的進價少10元.
(1)求商場第二批商品A的進價;
(2)商場同時銷售另一種熱銷商品B,已知商品B的進價與第二批商品A的進價相同,且最初銷售價為165元,每天能賣出125件,經市場銷售發現,若售價每上漲1元,其每天銷售量就減少5件,問商場該如何定售價,每天才能獲得最大利潤?并求出每天的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 為滿足社區居民健身的需要,市政府準備采購若干套健身器材免費提供給社區,經考察,勁松公司有![]() 兩種型號的健身器可供選擇.
兩種型號的健身器可供選擇.
(1)勁松公司2015年每套![]() 型健身器的售價為
型健身器的售價為![]() 萬元,經過連續兩年降價,2017年每套售價為
萬元,經過連續兩年降價,2017年每套售價為![]() 萬元,求每套
萬元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府經過招標,決定年內采購并安裝勁松公司![]() 兩種型號的健身器材共
兩種型號的健身器材共![]() 套,采購專項費總計不超過
套,采購專項費總計不超過![]() 萬元,采購合同規定:每套
萬元,采購合同規定:每套![]() 型健身器售價為
型健身器售價為![]() 萬元,每套
萬元,每套![]() 型健身器售價我
型健身器售價我![]() 萬元.
萬元.
①![]() 型健身器最多可購買多少套?
型健身器最多可購買多少套?
②安裝完成后,若每套![]() 型和
型和![]() 型健身器一年的養護費分別是購買價的
型健身器一年的養護費分別是購買價的![]() 和
和![]() .市政府計劃支出
.市政府計劃支出![]() 萬元進行養護.問該計劃支出能否滿足一年的養護需要?
萬元進行養護.問該計劃支出能否滿足一年的養護需要?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com