
【題目】如圖,在鈍角△ABC中,AB=5 cm,AC=10 cm,動點D從A點出發到B點止,動點E從C點出發到A點止,點D運動的速度為1 cm/秒,點E運動的速度為2 cm/秒,如果兩點同時運動,那么當以點A、D、E為頂點的三角形與△ABC相似時,運動的時間是( )
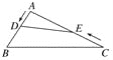
A. 2.5秒
B. 4.5秒
C. 2.5秒或4.5秒
D. 2.5秒或4秒
【答案】D
【解析】
運動t秒時,以點A、D、E為頂點的三角形與△ABC相似, AD=t,CE=2t,AE=10-2t,分兩種情況①△ADE∽△ABC②△ADE∽△ACB進行討論即可求出時間t.
如果兩點同時運動,設運動t秒時,以點A、D、E為頂點的三角形與△ABC相似,
則AD=t,CE=2t,AE=AC-CE=10-2t.
①當D與B對應時,有△ADE∽△ABC.
∴AD∶AB=AE∶AC,
∴t∶5=(10-2t)∶10,
∴t=2.5;
②當D與C對應時,有△ADE∽△ACB.
∴AD∶AC=AE∶AB,
∴t∶10=(10-2t)∶5,
∴t=4.
∴當以點A、D、E為頂點的三角形與△ABC相似時,運動的時間是2.5秒或4秒.
故選D.


科目:初中數學 來源: 題型:
【題目】某同學在利用描點法畫二次函數y=ax2+bx+c(a=0)的圖象時,先取自變量x的一些值,計算出相應的函數值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接著,他在描點時發現,表格中有一組數據計算錯誤,他計算錯誤的一組數據是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AC,BD相交于點O,點E是OA的中點,連接BE并延長交AD于點F,已知S△AEF=4,則下列結論:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正確的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正確的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AC,BD相交于點O,點E是OA的中點,連接BE并延長交AD于點F,已知S△AEF=4,則下列結論:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正確的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正確的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,BC=16 cm,AC=12 cm,點P從點B出發,沿BC以2 cm/s的速度向點C移動,點Q從點C出發,以1 cm/s的速度向點A移動,若點P、Q分別從點B、C同時出發,設運動時間為ts,當t=__________時,△CPQ與△CBA相似.
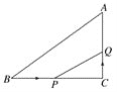
查看答案和解析>>
科目:初中數學 來源: 題型:
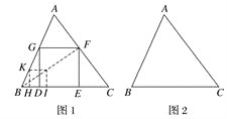
【題目】如圖1,給定銳角三角形ABC,小明希望畫正方形DEFG,使D,E位于邊BC上,F,G分別位于邊AC,AB上,他發現直接畫圖比較困難,于是他先畫了一個正方形HIJK,使得點H,I位于射線BC上,K位于射線BA上,而不需要求J必須位于AC上.這時他發現可以將正方形HIJK通過放大或縮小得到滿足要求的正方形DEFG.
閱讀以上材料,回答小明接下來研究的以下問題:
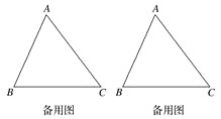
(1)如圖2,給定銳角三角形ABC,畫出所有長寬比為2:1的長方形DEFG,使D,E位于邊BC上,F,G分別位于邊AC,AB上.
(2)已知三角形ABC的面積為36,BC=12,在第(1)問的條件下,求長方形DEFG的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角△ABC中,邊BC長為12,高AD長為8
(1)如圖,矩形EFGH的邊GH在BC邊上,其余兩個頂點E、F分別在AB、AC邊上,EF交AD于點K
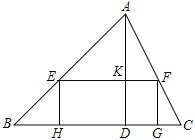
①求![]() 的值
的值
②設EH=x,矩形EFGH的面積為S,求S與x的函數關系式,并求S的最大值
(2)若ABAC,正方形PQMN的兩個頂點在△ABC一邊上,另兩個頂點分別在△ABC的另兩邊上,直接寫出正方形PQMN的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①所示,在△ABC中,點O是AC上一點,過點O的直線與AB,BC的延長線分別相交于點M,N.
【問題引入】
(1)若點O是AC的中點, ![]() ,求
,求![]() 的值;
的值;
溫馨提示:過點A作MN的平行線交BN的延長線于點G.
【探索研究】
(2)若點O是AC上任意一點(不與A,C重合),求證: ![]() ;
;
【拓展應用】
(3)如圖②所示,點P是△ABC內任意一點,射線AP,BP,CP分別交BC,AC,AB于點D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com