
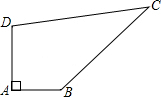
 如圖,某開發區計劃在一塊四邊形的空地ABCD上種植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,種植每平方米草皮的預算費用為300元,若第一年對草坪的保養費用占種植草皮總預算的4%,以后每年的保養費用都將在前一年的基礎上遞增2%,求第三年的草坪保養費用.
如圖,某開發區計劃在一塊四邊形的空地ABCD上種植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,種植每平方米草皮的預算費用為300元,若第一年對草坪的保養費用占種植草皮總預算的4%,以后每年的保養費用都將在前一年的基礎上遞增2%,求第三年的草坪保養費用. 分析 仔細分析題目,需要求得四邊形的面積才能求得結果.連接BD,在直角三角形ABD中可求得BD的長,由BD、CD、BC的長度關系可得三角形DBC為一直角三角形,DC為斜邊;由此看,四邊形ABCD由Rt△ABD和Rt△DBC構成,則容易求解,再進一步得到第三年的草坪保養費用.
解答  解:連接BD,
解:連接BD,
在Rt△ABD中,BD2=AB2+AD2=42+32=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BD2+BC2=CD2,
∴∠DBC=90°,
S四邊形ABCD=S△BAD+S△DBC=$\frac{1}{2}$×4×3+$\frac{1}{2}$×12×5=36.
所以需費用36×300×(4%+2%+2%)=864(元).
答:第三年的草坪保養費用是864元.
點評 此題考查了勾股定理的應用,通過勾股定理由邊與邊的關系也可證明直角三角形,這樣解題較為簡單.


科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,△ABC的三個頂點的坐標分別為A(1,-2),B(3,-1),C(1,-1).
如圖,在平面直角坐標系中,△ABC的三個頂點的坐標分別為A(1,-2),B(3,-1),C(1,-1).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
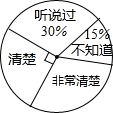 第十二屆全國人大四次會議審議通過的《中華人民共和國慈善法》已于今年9月1日正式實施,為了了解居民對慈善法的知曉情況,某街道辦從轄區居民中隨機選取了900名居民進行調查,并將調查結果制作成了如下不完整的統計圖和表:
第十二屆全國人大四次會議審議通過的《中華人民共和國慈善法》已于今年9月1日正式實施,為了了解居民對慈善法的知曉情況,某街道辦從轄區居民中隨機選取了900名居民進行調查,并將調查結果制作成了如下不完整的統計圖和表:| 聽說過 | 不知道 | 清楚 | 非常清楚 |
| A | B | 225 | C |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
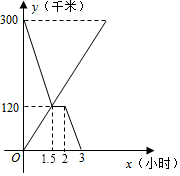 甲、乙兩車分別從A,B兩地同時出發相向而行,并以各自的速度勻速行駛,甲車與乙車相遇后休息半小時,再按原速度繼續前進到達B地;乙車從B地直接到達A地;兩車到達各自目的地后即停止.如圖是甲、乙兩車和B地的距離y(千米)與甲車出發時間x(小時)的函數圖象.
甲、乙兩車分別從A,B兩地同時出發相向而行,并以各自的速度勻速行駛,甲車與乙車相遇后休息半小時,再按原速度繼續前進到達B地;乙車從B地直接到達A地;兩車到達各自目的地后即停止.如圖是甲、乙兩車和B地的距離y(千米)與甲車出發時間x(小時)的函數圖象.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com