
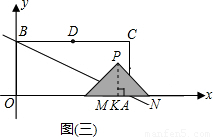
 x+b(b>0)分別交x軸,y軸于A,B兩點,以OA,OB為邊作矩形OACB,D為BC的中點.以M(4,0),N(8,0)為斜邊端點作等腰直角三角形PMN,點P在第一象限,設矩形OACB與△PMN重疊部分的面積為S.
x+b(b>0)分別交x軸,y軸于A,B兩點,以OA,OB為邊作矩形OACB,D為BC的中點.以M(4,0),N(8,0)為斜邊端點作等腰直角三角形PMN,點P在第一象限,設矩形OACB與△PMN重疊部分的面積為S. x+b(b>0)上存在點Q,使∠OQM等于90°,請直接寫出b的取值范圍.
x+b(b>0)上存在點Q,使∠OQM等于90°,請直接寫出b的取值范圍.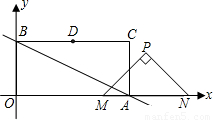
 NM=2,進而可求KO=6,所以P(6,2);
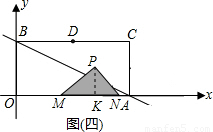
NM=2,進而可求KO=6,所以P(6,2); (2b-4)2;當3<b<4時,重合部分是一個四邊形,因此可設AC交PN于H,四邊形的面積=三角形PMN的面積-三角形HAN的面積,因為NA=HA=8-2b,所以S=-2(4-b)2+4,當b≥4時,重合部分就是直角三角形PMN,所以S=4.
(2b-4)2;當3<b<4時,重合部分是一個四邊形,因此可設AC交PN于H,四邊形的面積=三角形PMN的面積-三角形HAN的面積,因為NA=HA=8-2b,所以S=-2(4-b)2+4,當b≥4時,重合部分就是直角三角形PMN,所以S=4. x+b(b>0)上存在點Q,使∠OQM等于90°,利用90°的圓周角對的弦是直徑,所以以OM為直徑作圓,當直線y=-
x+b(b>0)上存在點Q,使∠OQM等于90°,利用90°的圓周角對的弦是直徑,所以以OM為直徑作圓,當直線y=- x+b(b>0)與此圓相切時,求得的就是b的最大值,而此時b=
x+b(b>0)與此圓相切時,求得的就是b的最大值,而此時b=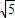 +1;
+1;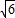 .
. NM=2,
NM=2, (2b-4)2=2b2-8b+8,
(2b-4)2=2b2-8b+8,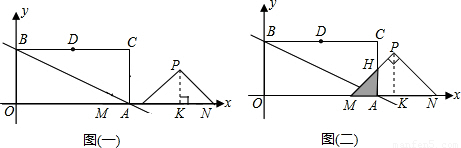
 x+b(b>0)與圓相切時,b=
x+b(b>0)與圓相切時,b= +1,如圖(五);
+1,如圖(五); x),因為∠OQM=90°,O(0,0),M(4,0)所以OQ2+QM2=OM2,
x),因為∠OQM=90°,O(0,0),M(4,0)所以OQ2+QM2=OM2, x)2]+[(x-4)2+(b-
x)2]+[(x-4)2+(b- x)2]=42,
x)2]=42, x2-(2b+8)x+2b2=0,
x2-(2b+8)x+2b2=0, x2-(b+4)x+b2=0,
x2-(b+4)x+b2=0, ≤b≤1+
≤b≤1+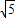 ,由于b>0,所以0<b≤1+
,由于b>0,所以0<b≤1+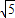 .
.
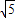 +1;
+1;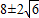 .
.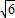 .
.

 每日10分鐘口算心算速算天天練系列答案
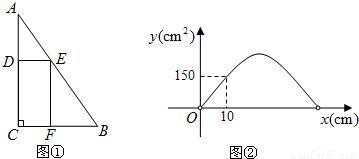
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(09)(解析版) 題型:解答題
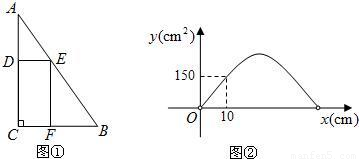
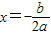 時,y最大(小)值=
時,y最大(小)值=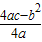 .)
.)
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《反比例函數》(05)(解析版) 題型:解答題
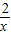 (x<0)的圖象于B,交函數y=
(x<0)的圖象于B,交函數y=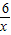 (x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.
(x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.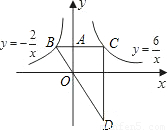
查看答案和解析>>
科目:初中數學 來源:2010年廣東省梅州市數學總復習測試卷(4) 函數(解析版) 題型:解答題
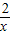 (x<0)的圖象于B,交函數y=
(x<0)的圖象于B,交函數y=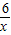 (x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.
(x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.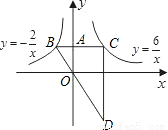
查看答案和解析>>
科目:初中數學 來源:2007年吉林省長春市中考數學試卷(解析版) 題型:解答題
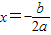 時,y最大(小)值=
時,y最大(小)值=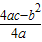 .)
.)
查看答案和解析>>
科目:初中數學 來源:2007年吉林省長春市中考數學試卷(解析版) 題型:解答題
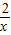 (x<0)的圖象于B,交函數y=
(x<0)的圖象于B,交函數y=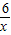 (x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.
(x>0)的圖象于C,過C作y軸的平行線交BO的延長線于D.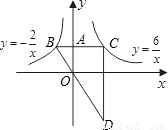
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com