
【題目】根據題意解答
(1)如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分別是BC、CD上的點,且∠EAF=60°,延長FD到點G,使DG=BE,連接AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得線段BE、EF、FD之間的數量關系為 .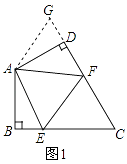
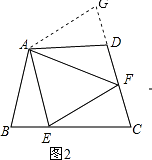
(2)如圖2,在四邊形ABCD中,AB=AD,∠B+∠D=180°,E、F分別是BC、CD上的點,且∠EAF= ![]() ∠BAD,線段BE、EF、FD之間存在什么數量關系,為什么?
∠BAD,線段BE、EF、FD之間存在什么數量關系,為什么?
(3)如圖3,點A在點O的北偏西30°處,點B在點O的南偏東70°處,且AO=BO,點A沿正東方向移動249米到達E處,點B沿北偏東50°方向移動334米到達點F處,從點O觀測到E、F之間的夾角為70°,根據(2)的結論求E、F之間的距離.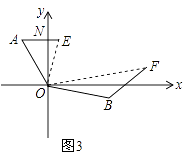
【答案】
(1)EF=BE+DF
(2)
解:EF=BE+DF仍然成立.
證明:如圖2,延長FD到G,使DG=BE,連接AG,
∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,
在△ABE和△ADG中,
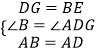 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
 ,
,
∴△AEF≌△GAF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF
(3)
解:如圖3,連接EF,延長AE、BF相交于點C,
∵∠AOB=20°+90°+(90°﹣60°)=140°,
∠EOF=70°,
∴∠EOF= ![]() ∠AOB,
∠AOB,
又∵OA=OB,
∠OAC+∠OBC=(90°﹣20°)+(60°+50°)=180°,
∴符合探索延伸中的條件,
∴結論EF=AE+BF成立,
即EF=583米.

【解析】解:(1)EF=BE+DF;
證明:如圖1,延長FD到G,使DG=BE,連接AG,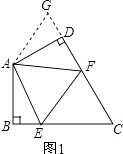
在△ABE和△ADG中, ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中, ,
,
∴△AEF≌△GAF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
所以答案是:EF=BE+DF


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A、B、C、D在同一條直線上,點E、F分別在直線AD的兩側,且AE=DF,∠A=∠D,AB=DC.
(1)求證:△ACE≌△DBF;
(2)求證:四邊形BFCE是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在新晚報舉辦的“萬人戶外徒步活動”中,為統計參加活動人員的年齡情況,從參加人員中隨機抽取了若干人的年齡作為樣本,進行數據統計,制成如圖的條形統計圖和扇形統計圖(部分). 
(1)本次活動統計的樣本容量是多少?
(2)求本次活動中70歲以上的人數,并補全條形統計圖;
(3)本次參加活動的總人數約為12000人,請你估算參加活動人數最多的年齡段的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標分別為:A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 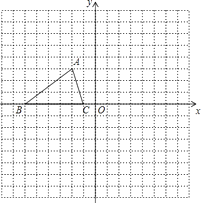
(1)將△ABC沿y軸翻折,畫出翻折后的△A1B1C1 , 點A的對應點A1的坐標是
(2)△ABC關于x軸對稱的圖形△A2B2C2 , 直接寫出點A2的坐標
(3)若△DBC與△ABC全等(點D與點A重合除外),請直接寫出滿足條件點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某人沿一條直路行走,此人離出發地的距離![]() 千米
千米![]() 與行走時間
與行走時間![]() 分鐘
分鐘![]() 的函數關系如圖所示,請根據圖象提供的信息回答下列問題:
的函數關系如圖所示,請根據圖象提供的信息回答下列問題:
![]() 此人離開出發地最遠距離是______ 千米;
此人離開出發地最遠距離是______ 千米;
![]() 此人在這次行走過程中,停留所用的時間為______ 分鐘;
此人在這次行走過程中,停留所用的時間為______ 分鐘;
![]() 由圖中線段OA可知,此人在這段時間內行走的速度是每小時______ 千米;
由圖中線段OA可知,此人在這段時間內行走的速度是每小時______ 千米;
![]() 此人在120分鐘內共走了______ 千米.
此人在120分鐘內共走了______ 千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
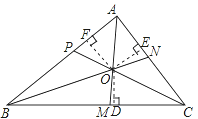
【題目】閱讀并理解下面的證明過程,并在每步后的括號內填寫該步推理的依據.
已知:如圖,AM,BN,CP是△ABC的三條角平分線.
求證:AM、BN、CP交于一點.
證明:如圖,設AM,BN交于點O,過點O分別作OD⊥BC,OF⊥AB,垂足分別為點D,E,F.
∵O是∠BAC角平分線AM上的一點( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分線( ),
∴O在CP上( ).
因此,AM,BN,CP交于一點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直線AG分別交DE、BC于M、N兩點.若∠B=90°,AB=4,BC=3,EF=1,則BN的長度為何?( ) 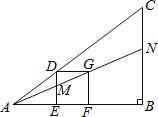
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com