如圖，小華發現電線桿AB的影子落在土坡的坡面CD和地面BC上，量得CD=8m,BC=20m,CD與地面成30°角，且此時測得1米木桿的影長為2m,則電線桿的高度為（ ）
A．14m B．28m C．(14+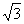
)m D．(14+
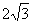)m
閱讀快車系列答案科目：初中數學 來源： 題型：
實際情境
某中學九年級學生步行到郊外春游．一班的學生組成前隊，速度為4 km/h，二班的學生組成后隊，速度為6 km/h．前隊出發1 h后，后隊才出發，同時，后隊派一名聯絡員騎自行車在兩隊之間不間斷地來回進行聯絡，他騎車的速度為12 km/h．
數學研究
若不計隊伍的長度，如圖，折線A-B-C、A-D-E分別表示后隊、聯絡員在行進過程中，離前隊的路程y（km）與后隊行進時間x（h）之間的部分函數圖象．
（1）求線段AB對應的函數關系式；
（2）求點E的坐標，并說明它的實際意義；
（3）聯絡員從出發到他折返后第一次與后隊相遇的過程中，當x為何值時，他離前隊的路程與他離后隊的路程相等？
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，在平面直角坐標系xoy中，菱形ABDC的邊AB在x軸上，頂點C在y軸上，A（-6,0），C（0,8），拋物線y=ax2﹣10ax+c經過點C，且頂點M在直線BC上，則拋物線解析式為 ；若點P在拋物線上且滿足S△PBD=S△PCD，則點P的坐標為 。
查看答案和解析>>
科目：初中數學 來源： 題型：
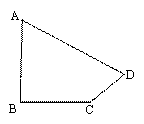
有一副直角三角板，在三角板ABC中,∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4,DE=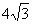
，將這副直角三角板按如圖(1)所示位置擺放,點B與點F重合，直角邊BA與FD在同一條直線上，現固定三角板ABC，將三角板DEF沿射線BA方向平行移動，當點F運動到點A時停止運動。
(1)如圖⑵，當三角板DEF運動到點D與點A重合時，設EF與BC交于點M，則∠EMC= 度；
(2)如圖⑶，在三角板DEF運動過程中,當EF經過點C時,求FC的長；
(3)在三角板DEF運動過程中，設BF=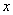
，兩塊三角板重疊部分面積為
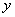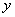，求與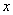的函數解析式，并求出對應的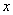取值范圍。（13南充卷改編）
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，在⊿ABC中，∠ABC和∠ACB的平分線相交于點O，過點O作EF∥BC交AB于E，交AC于F，過點O作OD⊥AC于D。下列四個結論：
①以E為圓心、BE為半徑的圓與以F為圓心、CF為半徑的圓外切；
②∠BOC=90°+
∠A；
③EF不能成為⊿ABC的中位線；
④設OD=m,AE+AF=n,則S⊿AEF =mn.
其中正確的結論是：
A．①②③ B．①②④ C．②③④ D．①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，再從0，3，-1中選擇一個合適的a的值代入求值。
的積為正整數的數是____________（寫出一個即可）
，BE=2，則tan∠DBE的值是（ ）
B．2 C．
D．
