
【題目】如圖,在矩形ABCD中,AB=6cm,BC=12cm,點P從點A出發沿AB以1cm/s的速度向點B移動;同時,點Q從點B出發沿BC以2cm/s的速度向點C移動.設運動時間為t秒.
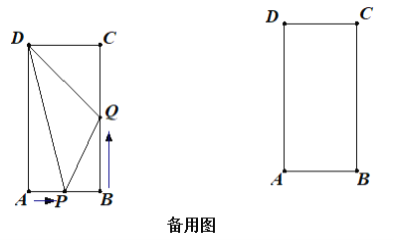
(1)當t=2時,△DPQ的面積為 cm2;
(2)在運動過程中△DPQ的面積能否為26cm2?如果能,求出t的值,若不能,請說明理由;
(3)運動過程中,當 A、P、Q、D四點恰好在同一個圓上時,求t的值;
(4)運動過程中,當以Q為圓心,QP為半徑的圓,與矩形ABCD的邊共有4個交點時,直接寫出t的取值范圍.
【答案】(1)28;(2)△DPQ的面積不可能為26cm2;(3)t=6或![]() 時A、P、Q、D四點恰好在同一個圓上;(4)當
時A、P、Q、D四點恰好在同一個圓上;(4)當![]() <t<
<t<![]() 時,⊙Q與矩形ABCD的邊共有四個交點.
時,⊙Q與矩形ABCD的邊共有四個交點.
【解析】
(1)根據運動速度表示出長度,然后計算出三個直角三角形面積,再由矩形面積減去三個直角三角形面積就能得到△DPQ的面積;
(2)根據(1)總得出的面積計算方式,列出關于t的方程,通過判斷方程有無解來即可判斷;
(3)△DAP是直角三角形如果它的三個頂點都在圓上,可得DP是直徑,Q也要在圓上,那么△DQP也是直角三角形,通過勾股定理用t表示出DP、PQ、DQ,再由DP=PQ+DQ列出方程求解即可;
(4)判斷出⊙Q與邊AD相切和⊙Q過D點是從有4個交點變成3個交點的時刻,再根據半徑相等列出關于t的方程求解.
由題意得AP=![]() ,BQ=
,BQ=![]()
∴PB=AB-AP=6-2=4,CQ=CB-BQ=12-4=8
∴![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]()
∴![]() =
=![]() -
-![]() -
-![]() -
-![]() =72-12-8-24=28(cm2)
=72-12-8-24=28(cm2)
(2)法一:根據題意得
![]() =
=![]()
整理得![]()
∵ b2-4ac=-4<0,
∴方程無實數根
∴△DPQ的面積不可能為26cm2
法二:
![]() =
=![]()
當t=3時,△DPQ的面積有最小值為27 cm2
∴△DPQ的面積不可能為26cm2
(3)∵∠A=90°
∴A、P、D三點在以DP為直徑的圓上
若點Q也在圓上,則∠PQD=90°
∵PQ2=(6-t)2+(2t)2,DQ2=62+(12-2t)2,DP2=t2+122
當PQ2+DQ2= DP2,∠PQD=90°
∴(6-t)2+(2t)2+62+(12-2t)2= t2+122
解得t1=6,t2=![]()
∴t=6或![]() 時A、P、Q、D四點恰好在同一個圓上.
時A、P、Q、D四點恰好在同一個圓上.
(4)如右圖1,
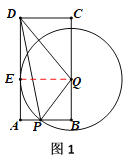
⊙Q與邊AD相切
過點Q作QE⊥AD
∵⊙Q與邊AD相切
∴QE=QP
62=(6-t)2+(2t)2
解得t1=0(舍去),t2=![]()
如右圖2,

⊙Q與過點D
則QD=QP
(6-t)2+(2t)2=62+(12-2t)2
![]() (舍去)
(舍去)
∴當![]() <t<
<t<![]() 時,⊙Q與矩形ABCD的
時,⊙Q與矩形ABCD的
邊共有四個交點.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,過點O作OD⊥AB,交BC的延長線于D,交AC于點E,F是DE的中點,連接CF.
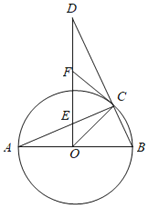
(1)求證:CF是⊙O的切線.
(2)若∠A=22.5°,求證:AC=DC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D是BC的中點,E是AD的中點,過點A作AF∥BC交BE的延長線于點F.
(1)求證:△AEF≌△DEB;
(2)求證:四邊形ADCF是菱形.
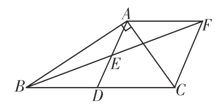
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.

(1)判斷直線CD和⊙O的位置關系,并說明理由;
(2)過點B作⊙O的切線BE交直線CD于點E,若BE=5,CD=8,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
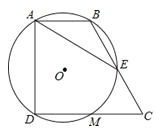
【題目】如圖,在四邊形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,過A,B,D三點的⊙O分別交BC,CD于點E,M,下列結論:
①DM=CM;②弧AB=弧EM;③⊙O的直徑為2;④AE=AD.
其中正確的結論有______(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
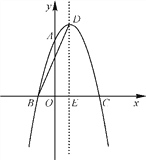
【題目】如圖,拋物線y=ax2+2x+c經過點A(0,3),B(-1,0),請回答下列問題:
(1)求拋物線對應的二次函數的表達式;
(2)拋物線的頂點為D,對稱軸與x軸交于點E,連接BD,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程 kx2+(2k+1)x+k+2=0.
(1)若該方程有兩個不相等的實數根,求k的取值范圍;
(2)若該方程的兩根x1、x2滿足![]() =-3,求k的值.
=-3,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在ABCD中,∠BAD的平分線交直線BC于點E,交直線DC于點F.
(1)在圖1中證明CE=CF;
(2)若∠ABC=90°,G是EF的中點(如圖2),直接寫出∠BDG的度數;
(3)若∠ABC=120°,FG∥CE,FG=CE,分別連接DB、DG(如圖3),求∠BDG的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com