Question

如圖，AB∥DF，AC⊥BC于C，BC與DF交于點E，若∠A=20°，則∠CEF等于

1. A.
   110°
2. B.
   100°
3. C.
   80°
4. D.
   70°

Answer 1

A
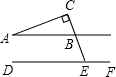
分析：如圖，由AC⊥BC于C得到△ABC是直角三角形，然后可以求出∠ABC=180°-∠A-∠C=180°-20°-90°=70°，而∠ABC=∠1=70°，由于AB∥DF可以推出∠1+∠CEF=180°，由此可以求出∠CEF．
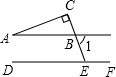
解答：解：∵AC⊥BC于C，
∴△ABC是直角三角形，
∴∠ABC=180°-∠A-∠C=180°-20°-90°=70°，
∴∠ABC=∠1=70°，
∵AB∥DF，
∴∠1+∠CEF=180°，
即∠CEF=180°-∠1=180°-70°=110°．
故選A．
點評：本題比較簡單，考查的是平行線的性質及直角三角形的性質．